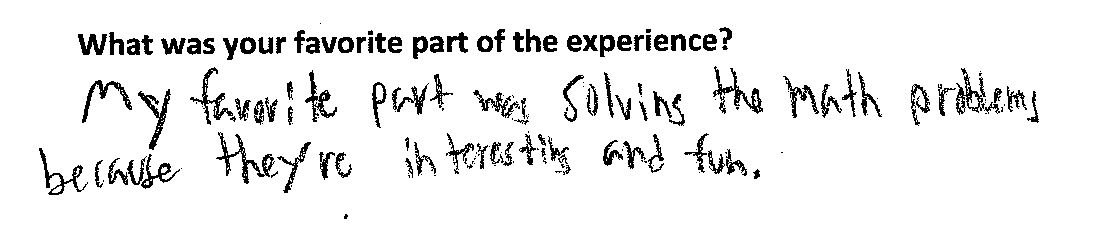Building on what we learned last summer, we made key changes to our online tools and other program elements to build a strong community and encourage students to dive deep into problem solving this summer. After the program, Ayaan told us, “This summer made me realize that the math I enjoy is the creative, puzzling kind.” Here are some highlights…
Saturday Classes at BEAM LA
BEAM Discovery LA: A fantastic first week
The Second Annual BEAM Los Angeles Math Competition
Kenny, Mayisa, and Adib were the top three individual competitors. Adib answered 17 of 18 questions correctly in the individual round!
On Saturday, 60 middle schoolers and their coaches joined BEAM for the second ever BEAM Los Angeles Math Competition. Of these, fully half (30 students!) attended BEAM 6 last summer.
The competition featured an Individual Round and a Team Round along with time to share solutions and an awards ceremony. Awards were given to the top three individuals, the top three teams, and the top school overall (based on how their multiple teams did).
Want a feel for the competition? Here’s a question that stumped students during the team round:
What is the biggest number which can be evenly divided by 12 with no remainder that you can make by using each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 at most once?
Students clearly loved the event! Here is some of their feedback:
We’d like to thank 9 Dots who generously donated the space for the competition; thanks so much!
Thanks also to all the students and staff of Alliance Richard Merkin Middle School, Berendo Middle School, Clinton Middle School, Equitas Academy #2, Girls Academic Leadership Academy (GALA), Rise Kohyang Middle School, Synergy Kinetic Academy, UCLA Community School, and Virgil Middle School who joined us on Saturday! We hope you had as much fun as the BEAM staff did in organizing this event.
Missed out? Here are some of our favorite images from the event!
Last year, BEAM held one math competition for 37 students. This year, we will be holding two and we can’t wait to see how many students show up for our spring competition! See you then!
What do 6th graders love about BEAM? Open Math Time!
With BEAM 6 Los Angeles' first two weeks in the book, we thought we'd take a minute to talk about one of the students' favorite parts of the day: Open Math Time! Every day at BEAM 6 includes four hours of academics: two hours of class and two hours of Open Math Time (OMT). During OMT, students choose from a menu of options, or propose their own work. They can do basically anything mathematical! Students can work individually or in groups; as long as the time is productive, any arrangement is fair game! OMT exists for a number of reasons:
Zavier (BEAM '11), right, supports students in a BEAM 6 LA classroom.
- BEAM classes don't assign homework, because it just doesn't seem right for a summer program! But, it's important to practice new ideas to really learn them. So, students use some of their OMT for short, required Problem Sets (PSets) from each class.
- BEAM believes in flexibility and choice. We want students to build the best possible summer for themselves!
- Middle schoolers are learning a lot about themselves. Students may never have been given the flexibility to choose their groupings or tasks. This is a huge opportunity for growth.
- Strong mathematicians become stronger by spending more time on math. By sharing with students the joy of self-paced, self-directed learning, we give students the tools they need to challenge themselves to learn independently.
Ever since our first summer of BEAM 6, students have raved about OMT. It becomes many students' favorite part of the day. And our BEAM 6 LA 2018 students are no different! Here are some reviews from our early program survey:
As you can see from the check boxes. students have a suggested menu of options for how to spend their OMT. Most students chose the following options:
PSets From Class
Every member of the faculty gives students about 15 minutes worth of extra work at the end of each class in the form of problem sets. Problem sets (PSets) are designed to help students practice and solidify new skills, extend understanding, and explore curiosity. For example, a student in a KenKen class might solve a more challenging puzzle, while a student learning to program in Python might add a new command to the program they're writing. Students working on PSets can head to their teacher's classroom to chat about the work and ask for support.
Want a flavor of a PSet? Here are some sample problems from two of our classes:
Exponents: The Super-Powers of Numbers
Find a number with five or more digits, all 0s and 1s, that is 7 in Z11 (in other words, it has a remainder of 7 when divided by 11).
Voting: How to Run a Country
A group of 4 friends want to do the same activity during activity time. Their options are to do any of the following: soccer (S), drama (D), frisbee (F), board games (B), or painting (P) and they decide to use Borda Count to decide the activity they should do. Consider the table of preferences below:
a) 5 points are assigned to a 1st place vote, 4 points to a 2nd place vote etc. What activity is the Borda count winner in this instance? (Make sure to give the Borda scores to justify your answer).
b) Is it possible for only one person to changing their ranking (in any way) so that painting is the only Borda count winner? If so, give the person and their new ranking and the new Borda counts of each alternative. If it is not possible, thoroughly explain why it is not possible.
100 Problem Challenge
Students work on a problem during OMT with their counselor Paula, right under the 100 problem board.
This is exactly what it sounds like: a hundred problems selected by Dan Zaharopol (BEAM Founder and the Executive Diretor of the Art of Problem Solving Initiative, Inc.) to challenge the students mathematically and bring them just to the edge of mathematical proof. There’s a big board with 100 spaces for the 100 problems, and we write in the names of students who’ve completed problems. If all 100 are solved before the end of week 5, the entire program wins a prize!
Try out a sample problem for yourself:
Problem 1
A friend tells me that she has three children, and that if you multiply their three ages you get 72. “I don’t have enough information to figure out how old they are!” I reply.
“All right,” she says, “if you add their ages, you get the street number from my address.”
I know where she lives, so I do some calculations. “I still don’t know how old they are!” I reply.
“Well,” she replies, “the oldest is really good at chess.”
Now I know how old they are. How old are her children, and what is her street address?
The state of the 100 problem challenge at the end of week 1.
Art of Problem Solving/Alcumus
Students, hard at work!
Another major goal of BEAM is that our students (new to enrichment math) have access to the same resources and opportunities that other middle schoolers all over the country already have! So, we connect them all with accounts for the Art of Problem Solving (AoPS), and encourage students to start with Alcumus. Alcumus is a free, self-paced tool that works students through math skills, starting at pre-algebra. It's fun and it's something students can use for years to come!
Becoming familiar with AoPS and Alcumus know will have major benefits to BEAM 6 alums during 7th grade, as AoPS offers a free, online pre-algebra course to any BEAM 6 alum who completes the Alcumus pre-work to demonstrate to BEAM that they plan to take the course seriously. And as our students age, we sign individual students up for AoPS classes whenever they need an enrichment boost, and are looking to challenge themselves (the combinatorics and number theory classes are a particular hit!).
We're so glad students are enjoying OMT and the rest of BEAM 6. It's clear that BEAM 6 Los Angeles is off to an incredible start! Want to read more? Check out what our own Executive Director, Dan Zaharopol, had to say on his blog:
BEAM LA Hosts a Math Competition
On Saturday, December 2nd, BEAM LA hosted a math competition at the University of Southern California (USC) for partner middle school students. Forty students from grades 6-8 participated in a group round and individual round, solving puzzly math problems alongside their peers.
The students were deeply engaged in the problems; some students continued working on the problems during lunch and break time, even after submitting their answers! Here's what some students had to say:
-Abraham, 6th grader
-Ava, 6th grader
Isabella, 7th grader
There were two problems in the individual round that stumped all the participants. Can you solve one?
How many whole numbers from 100 to 999 (including 100 and 999) have no two digits next to each other that are the same? (For example, 121 is good, but 322 and 112 are not).
Pictured below are the top 2 performers from each grade level. The top winning teams were from UCLA CS and Synergy Kinetic.
A big thanks goes to: all of our participating schools and students, the USC Math Department and Viterbi School EOP for sponsoring the event, and MATHCOUNTS and The Art of Problem Solving for allowing us to use their problems in the competition.