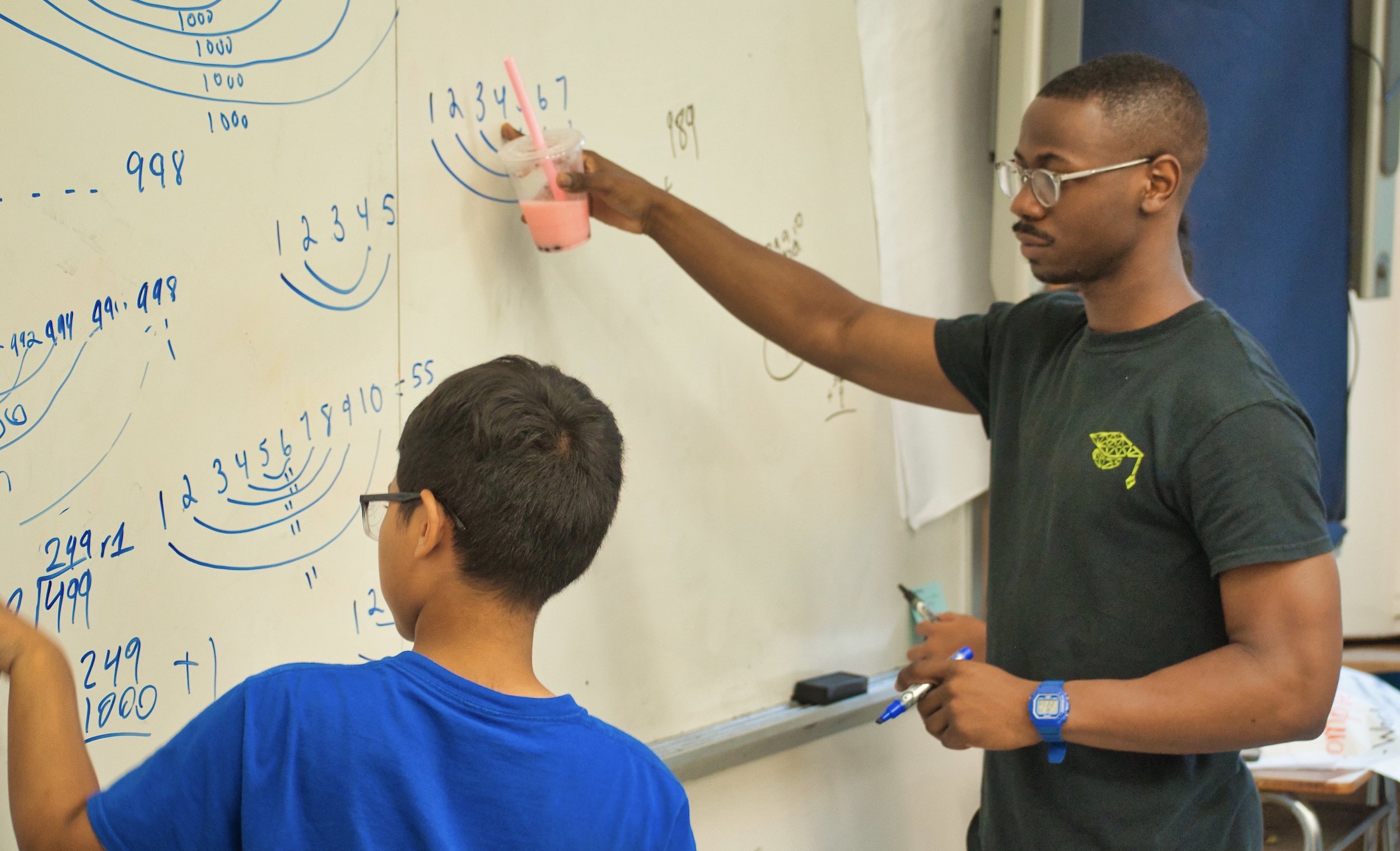... And Now for Some Math

Try your hand at a Problem of the Week from BEAM Discovery (our summer program for rising 7th graders)! The Problem of the Week gives students a chance to explore interesting math outside of their classes, either on their own or in collaboration with others. It also provides an opportunity to build relationships with site leadership (who usually grade the problems), and a chance for staff to celebrate persistence in problem solving. This summer, students who solved a Problem of the Week received a special badge. See if you can solve Week 4’s Problem of the Week!

Solution:

One of the BEAM Discovery students who solved this problem was Jayden. You can see his submission at the end of this post!

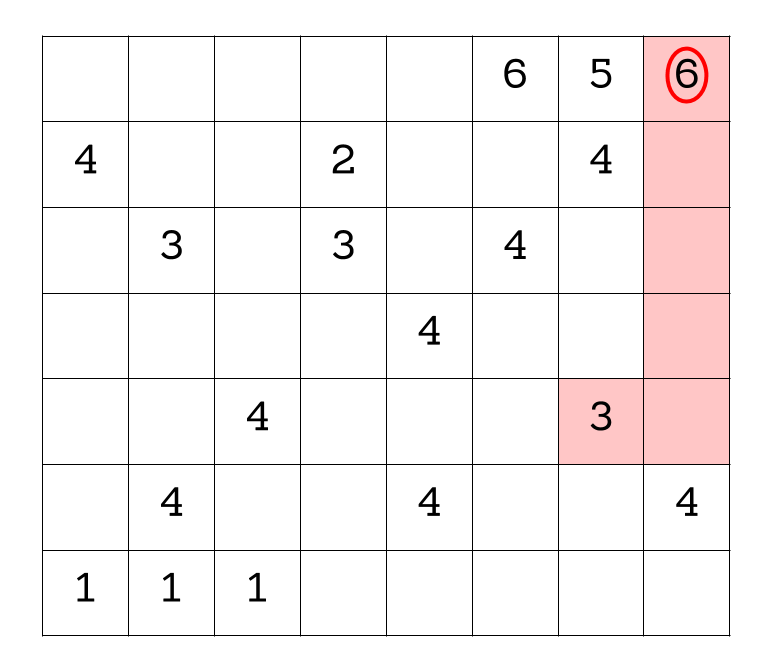
There are 56 squares in the grid, which has to also be equal to the number of regions times the number of squares in each region. Meanwhile, the sum of the numbers is 63, which has to also be equal to the number of regions times the sum in each region. This is where we can combine two facts to make the problem simpler: the number of regions must divide both 56 and 63! Since the only common divisors are 1 and 7 (and one region doesn't solve the problem), there must be 7 regions. Dividing, we see that each region has 56/7=8 squares, and the sum in each region is 63/7=9.

Now that we are satisfied that the only possible solution will have 7 regions with 8 squares in each region and each region should sum to 9, we still have the very tricky task of figuring out if we can actually come up with such a configuration. This seems like a pretty daunting task. One way to make it a little easier is to start with the squares containing large numbers (like 5 or 6) since there might be more limited options for the regions that contain them.

It also helps to lay out a couple of “rules” that help guide how we can build regions.

1. A number can’t be paired with a number that is “too far away.” Too far away means that it would take too many blocks to include it in the part of the region that is already determined, since each region can only be 8 blocks in total. For example, the 6 in the top right can’t be in the same region as the 1 in the bottom left, because it would take too many blocks to connect them.

2. Each region must contain exactly one odd number. Why? Because each region has to sum to 9, which is an odd number; therefore, it must contain at least 1 odd number. But there are exactly 7 odd numbers in total on the grid, so none of the 7 regions can contain more than one.

Just a note: To save time on the explanation, we're going to make a few simplifying guesses, but it is possible to solve the entire puzzle without having to make any guesses about how things come out!

First let’s think about the two 6’s, because those seem like they might be the easiest. Because the 6’s are the biggest numbers in the grid, and they can’t be paired with any 4’s or 5’s, this helps immediately narrow down our options. They also can’t be paired with any of the 1’s, according to rule 1, since the 1’s are too far away.

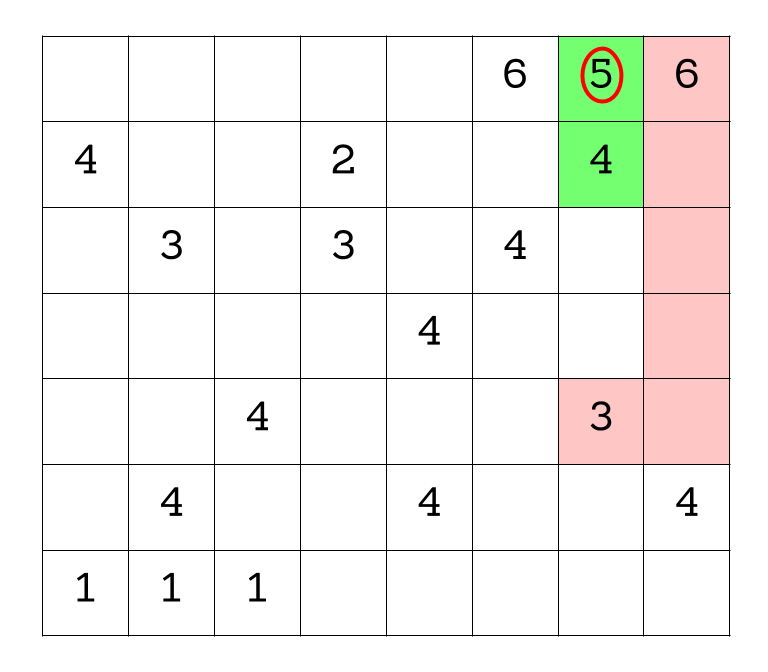
Starting with the 6 in the upper righthand corner, there is only one 3 available to be included in this region, as all the other 3’s are too far away/we would need to include another number in the region which would make it to have too high of a sum.

Now turning to the only 5 in the grid we know it must include the 4 immediately below it because that is the only direction we can expand this region without including a 6 and bumping our sum up to 11, which is too high.

Next I would like to tackle the 6 that is remaining but it is hard to figure out which 3 belongs in the same region as it since neither is too far away. So, let’s look at the 1’s. Because they are odd, each one has to be in its own region. And because they are adjacent, we have fewer directions we can go.

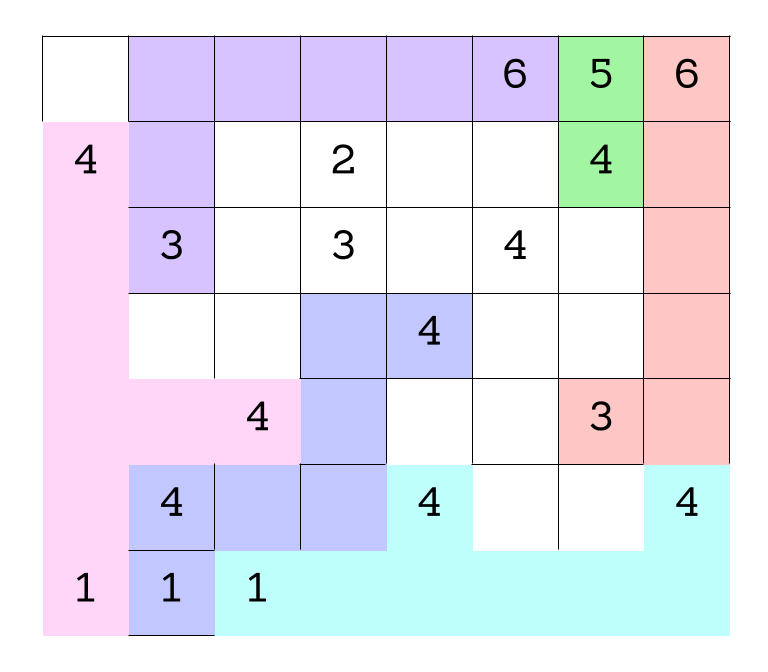
Starting with the 1 in the bottom lefthand corner, we know it has to include the two 4’s (indicated in the figure below). All the other even numbers are either too far away (shown in red) or if we included them in the new purple region we would cut off the other 1’s so that they would need to share a region, which we can’t do (we have highlighted those numbers in green). So, none of those numbers can be included in this region leaving only 2 available 4’s to be included in pink.

Moving on to the next 1 (circled in red) we see again most of the even numbers are too far away to be included in this blue region (in red). There is just one 4 that is close enough to work, but if we include it in blue the 1 that is leftover will be cut off from all but a single 4, which would not be a workable region. So, the green 4 can’t be included either, leaving us with the blue region shown below.

At this point you might be thinking,Wait! The green region has only two tiles, the pink region has 8, the salmon-colored region only has 6. Aren’t they all supposed to have 8 tiles in a region?

Well, that’s right, each region does need to have eight tiles in our final solution. But it is really hard to see how blank tiles should be assigned to make everything work out, so we will start by just figuring out which numbers should share a region, and then see if we can divvy up the blank tiles from there. That’s why our regions will each add up to 9 to start with, but they may not have 8 tiles in them just yet.

Now we just have one 1 left and two of the remaining even numbers (highlighted in red) are too far away. If we included the other 4 (highlighted in green) then we would end up cutting off the 4 in the bottom right corner. With just two of the 4’s left, we know that they should be included in the turquoise region below.

Now we can finally circle back to the remaining 6, and try to figure out which 3 it should be paired with. Now if we pair it with the right-most 3 (in green) we will cut off the remaining 4 from all the other numbers, which isn’t allowed. That leaves the 3 on the left, which we will include in the purple region.

The last numbers standing 2,3, and 4 of course must share a region. But now that we know which numbers share a region, let’s move on to expanding regions to have exactly 8 squares.

Two of the regions are already exactly 8 squares (pink and turquoise).

Now the only region the top left square can be included in is the purple region, which brings the purple region to a full 8 squares.

Now that the pink and purple regions are more settled we can tackle the last three numbers. We know they have to share a region (grey). The square outlined in red also has to be grey because if it was part of the blue region, then the blank square to the left of it would be cut off and couldn’t be added to any of the regions next to it.

With the four grey squares above filled in, we can complete the grey area, since all the blank squares to the left of the grey area have to be filled in grey and the 4 in grey has to be included in the grey region.

The green region must expand into the blank squares to the right and then down to keep it a single region of exactly 8 squares.

And with that we can complete the final region (salmon colored). Whew! What a process!?!

A few more questions

Now we can verify that this solution is indeed a solution, just by checking that each region does sum to 9 and each region does have exactly 8 squares. But another question you may be asking yourself, and what a mathematician might ask themselves about a solution like this, would be:

Is this the only solution (i.e. is it unique)? If it is the only solution, how could you show that it is the only one?

If you enjoyed solving this problem, you can tackle the additional questions above for some bonus fun. :)

Jayden’s Solution, BEAM Discovery 2020

This problem comes from USAMTS, a national math contest.

Thank you BEAM supporters!

Thanks to everyone who has contributed to BEAM!

Now that our summer programs are over, our students would like to tell you what they accomplished.

“I solved a lot of challenge problems with my friends.” —Ruth, BEAM Discovery

“I solved 12 problems in the 100 Problem Challenge.” — Vernon, BEAM Discovery

“I learned some coding and got WAY better at it. BEAM made me love math and realize my passion for it!” —Mia, BEAM Discovery

“This is my first ever program and I loved it! I’m glad that you helped support BEAM.” —Hayden, BEAM Discovery

“BEAM helped me see math in a whole different way. THANKS.” —Sanjana, BEAM Discovery

“BEAM is a glowing star.” (left) —Estefani, BEAM Discovery

“BEAM is out of this world.” (right) —Allison, BEAM Discovery

BEAM Discovery Uptown Day 18!

Students were busy on Day 18 of BEAM Discovery Uptown. After breakfast, some students started the day in the class Playing with Logic, where they explored the Shuttle Puzzle by becoming the puzzle pieces. (Classes at BEAM are unlike anything most students see at school. Other classes this week include Math for Pirates and Learning from The Number Devil.)

During Open Math Time, when students get to choose what math they work on, some students completed problem sets from their classes. Students are often encouraged to work together to find the answers.

In Applied Math, students talked about game strategies and how to win at games, like Nim. They asked the question, “Can strategies help you win even at a game like Rock, Paper, Scissors, that seems all about luck?” Yes, they decided, by doing things like looking for patterns in your opponent’s play. To test their theories, they squared off in a Rock, Paper, Scissors tournament!

Students checked out the 100 Problem Challenge. As of today, only one problem remains! If the students solve all 100, they win a special prize.

A group of students discussed Problem 74 with Xavier, a veteran faculty member.

Are you up to the challenge? Here’s Problem 74:

In Problem 53, you found a way to link three rings so that if you cut just one of the three rings, the other two would come apart.

In this problem, your goal is to do the same thing but with four rings. Together, all four should be linked. But cut any one of the four rings, and the other three should come apart. (Hint: try using pipe cleaners, like the students above, to help visualize the problem.)

Activities at Beam Discovery

Activities at BEAM Discovery’s Downtown site is one of the ways we unwind and socialize with each other. During Week 3 we were able to take great pictures of students and staff having a great time.

Basketball

Yu-Gi-Oh! Tournament

Kickball

Friendship Bracelet Making

A Day at BEAM Discovery

So what exactly happens at BEAM Discovery? Here’s a look at a typical day, featuring photos from BEAM Discovery’s Downtown NYC campus!

The morning starts with breakfast, followed by morning classes. BEAM believes in choice, so students pick classes, which might be “Beating Sherlock” or “Fractions, Puzzles, and Games.”

After class, students have an hour of Open Math Time, time where they can work on any math they choose, individually or in groups. They make sure to complete required PSets (problem sets) from class, and they can then explore challenges (the Problem of the Week or the 100 Problem Challenge), math books, coding websites, the Art of Problem Solving, and more.

After class, it’s on to activities! BEAM students get their choice of sports, board games, arts and crafts, and other creative activities. Recent hits included how to solve a Rubik’s cube, origami, anime club, and relay tic-tac-toe.

After activities, it’s off to lunch. BEAM pays for catered lunch from local restaurants every day. These photos are from empanada Thursday!

Most days, the afternoon block features an exact repeat of the morning block: class, open math time, activities. But one day each week, we have special afternoons, which feature Relays, a team-based math competition where students solve math challenges with some silliness mixed in. A recent problem required students to hum a tune their judge would recognize before they gave their math answer!

When the day wraps up, students join their travel groups to take the subway home and relax and recharge so their brains are fresh for another day at BEAM!

BEAM Discovery LA: A fantastic first week

Students did great work the first week of BEAM Discovery LA!

Each week students can choose to work on the Problem of the Week on their own or with others. The first week, 27 students solved the problem, 10 within the first two days!

Are you up to the challenge? Find out:

Is there a 10-digit number where the first digit is equal to how many 0s are in the number, the second digit is equal to how many 1s are in the number, the third digit is equal to how many 2s are in the number, all the way up to the last digit which is equal to how many 9s are in the number?

If yes, can you find all of them? If no, how do you know for sure?

Week 1 featured classes unlike anything most students see in school:

Elementary My Dear — Students explore different techniques to solve complicated riddles and learn how to apply them to tough mathematical problems.

Truth, Lies, and Logic — Welcome to the land of liars and truth-tellers. What can we figure out in such a crazy place, and how can it help us solve really difficult math problems? 

Fractions and Food — Students’ thinking about fractions (and, hmmm, food) is challenged.

Words Meet Numbers: An Algebra Story — Students learn how Algebra can translate words into numbers and vice versa.

When we asked our students what they thought about the classes, one told us (about Elementary My Dear): 

“One of the many topics that are good about this class is that they teach us how to use clues, vocabulary in word problems, and solve mysteries like a CSI. Also, the staff are really nice.”

Another student said (about Truth, Lies, and Logic):

“You get to learn many things and the problems get you frustrated meaning you'll just have to try harder.”

But it’s not all math all the time. Students also participated in fun activities like a Toy Story Marathon to prepare for the field trip to see Toy Story 4. 

Others played board games, challenging their friends and counselors to Uno, Connect 4, Settlers of Catan, and more. Students were also excited by our science activity where Skittles and M&Ms were placed in water and their color slowly seeped out to create beautiful designs.

Recruiting and Selecting BEAM Students: A First Hand Account

Today, we have a guest blog post from long-time BEAM volunteer, Maury Bohan, who is also a retired 6th grade math teacher. Maury accompanied our staff on an admissions school visit back in March and had the following to say about her experience. While BEAM’s admissions season is over (it runs January-March), we’re always thinking ahead to next year, when we can’t wait to meet 6th graders in Los Angeles and New York City who are applying to our entry level program, BEAM Discovery.

Early in March, on a Wednesday morning, I had the pleasure of joining Lynn Cartwright-Punnett at PS 171/Patrick Henry Preparatory School in East Harlem, which has been a BEAM partner school since 2014. I had wanted to participate in a visit to one of BEAM’s partner schools, and Lynn felt it would be beneficial if we used the visit as a chance to share details with our many volunteers, instructors, and supporters.

A 7th grader works on the Admissions Challenge.

We began the morning with eight 7th graders, two of whom attended last summer’s BEAM Discovery program. The goal was to check in on what the BEAM Discovery alumni were doing and also to identify any 7th graders who we had not met in 6th grade, who would benefit from joining our program, AND who could succeed despite not having attended last summer. Lynn shared the goals of the BEAM Pathway Program, which include “…going farther than you expect, learning more, and exploring new ideas.” In addition to the potentially overwhelming information that the students would be with BEAM all the way through college, she also tempted the young students with details about dorm life, field trips, and good, hard brain work. After responding to questions, Lynn handed out the Admissions Challenge — seven questions to be completed in 40 minutes, and explained that the goal is not to do all of it perfectly, but rather “to figure out what you can figure out.”

7th graders at another BEAM partner school, KIPP Infinity, tell their 6th grade colleagues about BEAM Discovery.

After the 7th graders left the room, we were joined by a new crew of about fifteen 6th graders. They were physically so much younger than the 7th graders — clearly still children — and obviously nervous. Lynn immediately put them at ease, asking what they already knew about BEAM Discovery — basically that it is a summer math program five days per week for five weeks. She shared the daily schedule, and the goal to challenge brains, to grow and do more than students could do before, and to be a member of a math-loving community. Again there was talk of preparation for college, in terms of how choosing courses and activities during the summer is a way to start building autonomy so as to eventually be ready for decision making in college. Lynn then handed out the Admissions Challenge, and reminded students that “The goal isn’t perfect work; it’s interesting work.”

Besides the results of the students’ work on the Admissions Challenge, there are a few other ways for them to demonstrate their potential as a BEAM student. They are all asked to share how they felt about the challenge and what they liked about it. They are also given some extra problems to do at home and send back, which can show readiness and interest, and allow students to perform while not under time pressure.

There is a third way that a student might earn some unofficial points toward gaining a slot in a BEAM program, and it was demonstrated after the sixth graders left us. Lynn earlier had an opportunity to quickly review the 7th graders’ responses to their Admissions Challenge and had asked the school contact person to bring one student back to our classroom for an interview. This would allow Lynn to ascertain whether the student is as ready for this summer’s 7th grade program as all the incoming alumni of last summer’s Discovery Program will be. I enjoyed listening first as the two of them chatted about school and math, and the student’s personal life. She shared that her life outside of school is mostly homework, supporting a younger sister’s homework, and church. She has never been outside of New York City, and wants to be a veterinarian when she grows up. What is she most concerned about in regards to BEAM’s summer program? That it is a sleep away program!

After chatting, Lynn and the student got down to work, discussing some great math problems. How encouraging it was for me to observe their back and forth, and the young lady’s willingness to draw conclusions, and then re-evaluate them given Lynn’s prodding. The student’s patience, persistence, and flexible thinking seemed to me qualities that will make her succeed, and that BEAM would benefit from. And this is where those unofficial points toward entrance come in to play. “Slant points” are like an additional note, one which this girl definitely received, that says if there is a tie for a slot at BEAM, this student has that “something extra” that makes her the preferred candidate.

As a retired teacher, I can’t imagine many more encouraging mornings than watching all of these 6th and 7th graders voluntarily meeting with a stranger to demonstrate their interest and talent in mathematical thinking. I can’t wait to hear which students are joining us this summer, and I look forward to seeing them grow and thrive through high school.

Maury works with Alberto and Rebecca on trivia questions at BEAM’s annual night of puzzles and trivia.

BEAM Discovery Family Lunch

On Saturday, May 4th we welcomed newly admitted BEAM Discovery students to the program with our annual Family Welcome Lunch. Students and their families got the chance to meet the BEAM full time and summer staff, other admitted students and learn more about what to expect in from the summer. Additionally, we invited BEAM alumni and parents to come share their experience during the summer. Check out some pictures of the event below:

If you did not get to attend the lunch or are interested in the event, check out the video below:

Infinities, Graph Theory, Game Theory, and Traveling Circuses: What Mathematicians Talk About When They Visit BEAM

This winter, BEAM is busy! We are busy hiring summer faculty, summer counselors, and other summer staff and even a few full time staff. But those aren’t the only positions we are looking to fill. Every summer we invite guest speakers to BEAM Summer Away and BEAM Discovery sites. Our invited speakers are talented mathematicians from around the world, and their talks are a window into the work of professional mathematicians, giving students an opportunity to learn new ideas from the wide world of mathematics. Some past speakers have focused on complex mathematical topics, while others share their day to day life as career mathematicians. As we line up further intriguing talks for this summer, now is a great moment to reflect on some of the lovely talks and mind-bending math our guest speakers shared with us last summer.

This past summer our guests included Dr. Edray H. Goins, Dr. Susan Loepp, Tai-Danae Bradley, and Darleen Perez-Lavin. They each presented a unique take on a mathematical topic and BEAM students got a kick out of what they had to share.

Edray confronted a complicated topic: infinities and cardinality. Though this topic is deep and challenging even for mathematics majors at top colleges and universities, Edray balanced the abstract ideas with concrete examples. He started with basic ideas and questions: What is a set? How can you count things in a set? How many subsets are there in a set with n elements? Then the talk got more abstract, and Edray lead students through a very enjoyable explanation of Cantor's famous theorem. Students had the chance to see how much there is to the mathematical world than just numbers, equations and geometry formulas.

BEAM values having guest talks that start out very friendly to students and then go off the deep end in mathematics a bit because they allow students to see just how serious and deep math can be!

Dr. Edray H. Goins is a Professor of Mathematics at Pomona College in Claremont, CA and president of the National Association of Mathematicians. Edray presented at BEAM Discovery Los Angeles.

Dr. Goins presents to the students at BEAM Summer Away during Vassar 2016. Edray has been a guest speaker at BEAM for three straight summers!

Dr. Susan Loepp, Chair and Professor of Mathematics, Williams College. Susan presented at BEAM Summer Away at Union College.

Susan introduced a team game that involved wearing hats. It costs money to play, but if you win, you get the cost doubled back.  Will you win or lose money in the long run? Susan gave student volunteers a chance to play the game (not with real money) and think about optimal strategies. After a lot of trial and error (and some inadvertent cheating), students claimed to Susan that they could win 50% of the time. But she said they could do better! The rest of the talk focused on independent and dependent probability and how those concepts impact game theory. Students found the session fun and silly, yet thought provoking. Many were still talking about it the next day!

Tai-Danae came into the room with lots of brightly colored cubes. The purpose? The Instant Insanity puzzle. Everyone got four cubes with each face colored in one of four different colors. The question: can you make a stack four cubes tall so that each side of the stack has one face of each color? With over 80,000 possible configurations, this is a big challenge, but using the tools of graph theory you can solve it quickly! If you're curious, Tai-Danae also presented it on PBS Infinite Series and you can take a look and try it yourself.

Tai-Danae Bradley is a PhD candidate in mathematics at the CUNY Graduate Center, and creator of the intriguing math blog: https://www.math3ma.com/. Tai-Danae presented at BEAM Discovery NYC Uptown.

Darleen Perez-Lavin is a SMART fellow and graduate student at the University of Kentucky. Her talk was based on quantum computing research at Fermi National Accelerator Laboratory. Darleen presented at BEAM Summer Away at Union College.

Darleen gave a presentation on the Traveling Circus Problem, a more general version of the well-known and very difficult Traveling Salesman Problem (so well known and difficult that the University of Waterloo has a whole website devoted to it). Darleen presented new research on how this problem is related to quantum physics. Her talk gave a glimpse into how pure mathematics can have applied applications. The ideas jumped from Euler's solution to the Seven Bridges of Königsberg problem to talking about modern physics! Students interested in applied mathematics were especially fascinated.

We can’t wait to see all the amazing talks that this upcoming summer has in store. And if you enjoy cool math (and aren’t quite as busy as BEAM is at the moment), we encourage you explore the topics touched on in the talks above.

BEAM students play a game during Dr. Susan Loepp’s math talk at BEAM 2018.

New Names, Same Great Programs!

At BEAM Discovery 2018, two students work together to solve a math problem.

Here at BEAM we are incredibly excited for the new year! We are already diving into hiring our summer staff and admissions for our summer programs. We anticipate many highs and lows as waves of college and high school acceptances for our current BEAM students roll in. As BEAM braces for all the fresh and familiar that the new year is bound to bring, this seems like the perfect time to debut our programs’ shiny new names. Throughout the fall of 2018, BEAM staff spent some time carefully thinking about how to update our program names to make sure they truly showcase what our programs are about. After much thought, we are excited to announce our new program titles.

Our summer program after 6th grade, formerly BEAM 6, will now be known as BEAM Discovery. We’ve made an even bigger change to our other program, BEAM 7. Recognizing that we now support students from 7th grade through college, we’ve renamed it the BEAM Pathway Program, which comprises the summer program and all that comes beyond. The idea behind these new names is that first you discover BEAM, then you walk down the pathway with us, which culminates in college graduation! There are many steps in the BEAM Pathway Program, each with its own name: BEAM Summer Away (the residential summer program), BEAM 8th Grade Support, BEAM HS Support, BEAM College Prep, and BEAM College Support.

Of course, being our usual nerdy selves, we had to throw around some rather mathy name suggestions before we settled on this sensible line up. While we ended up choosing names that are a little more practical and prosaic, we felt these whimsical, mathematical suggestions deserved an honorable mention as runners-up:

• 7th Grade Summer Program: BEAM Axiom

• 8th Grade Saturdays: BEAM Hypothesis

• 9th-10th Grade Saturdays: BEAM Conjecture

• 11th-12th Grade Saturdays: BEAM Infinity

• College Support: BEAM Omega

As fun as these names were, we wanted to make sure that our new names clearly conveyed what each step of our pathway is really about. We believe we have captured each BEAM program with the name we have chosen, and we are excited to fully transition to using our up-to-date names here in 2019!

Students at BEAM Summer Away 2018 explore a waterfall together!