... And Now for Some Math
Try your hand at a Problem of the Week from BEAM Discovery (our summer program for rising 7th graders)! The Problem of the Week gives students a chance to explore interesting math outside of their classes, either on their own or in collaboration with others. It also provides an opportunity to build relationships with site leadership (who usually grade the problems), and a chance for staff to celebrate persistence in problem solving. This summer, students who solved a Problem of the Week received a special badge. See if you can solve Week 4’s Problem of the Week!
Solution:
One of the BEAM Discovery students who solved this problem was Jayden. You can see his submission at the end of this post!
There are 56 squares in the grid, which has to also be equal to the number of regions times the number of squares in each region. Meanwhile, the sum of the numbers is 63, which has to also be equal to the number of regions times the sum in each region. This is where we can combine two facts to make the problem simpler: the number of regions must divide both 56 and 63! Since the only common divisors are 1 and 7 (and one region doesn't solve the problem), there must be 7 regions. Dividing, we see that each region has 56/7=8 squares, and the sum in each region is 63/7=9.
Now that we are satisfied that the only possible solution will have 7 regions with 8 squares in each region and each region should sum to 9, we still have the very tricky task of figuring out if we can actually come up with such a configuration. This seems like a pretty daunting task. One way to make it a little easier is to start with the squares containing large numbers (like 5 or 6) since there might be more limited options for the regions that contain them.
It also helps to lay out a couple of “rules” that help guide how we can build regions.
A number can’t be paired with a number that is “too far away.” Too far away means that it would take too many blocks to include it in the part of the region that is already determined, since each region can only be 8 blocks in total. For example, the 6 in the top right can’t be in the same region as the 1 in the bottom left, because it would take too many blocks to connect them.
Each region must contain exactly one odd number. Why? Because each region has to sum to 9, which is an odd number; therefore, it must contain at least 1 odd number. But there are exactly 7 odd numbers in total on the grid, so none of the 7 regions can contain more than one.
Just a note: To save time on the explanation, we're going to make a few simplifying guesses, but it is possible to solve the entire puzzle without having to make any guesses about how things come out!
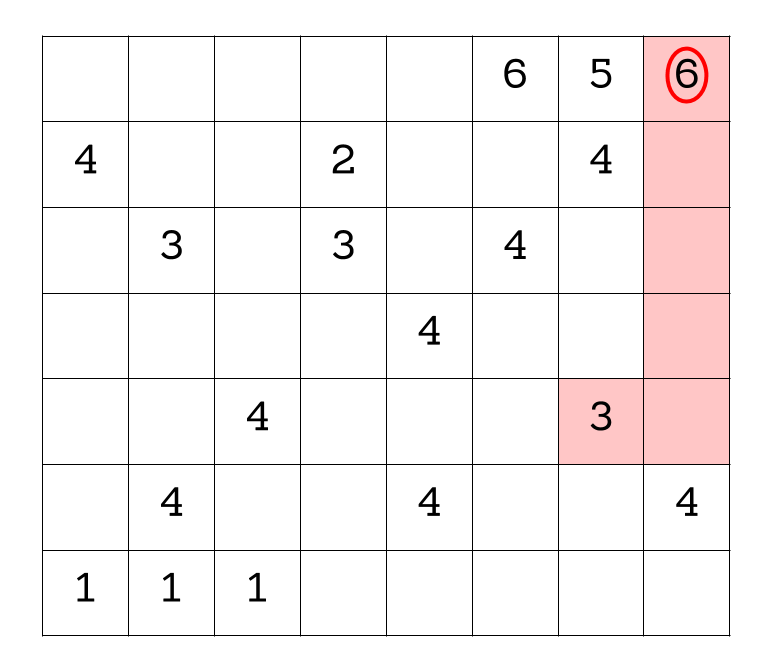
First let’s think about the two 6’s, because those seem like they might be the easiest. Because the 6’s are the biggest numbers in the grid, and they can’t be paired with any 4’s or 5’s, this helps immediately narrow down our options. They also can’t be paired with any of the 1’s, according to rule 1, since the 1’s are too far away.
Starting with the 6 in the upper righthand corner, there is only one 3 available to be included in this region, as all the other 3’s are too far away/we would need to include another number in the region which would make it to have too high of a sum.
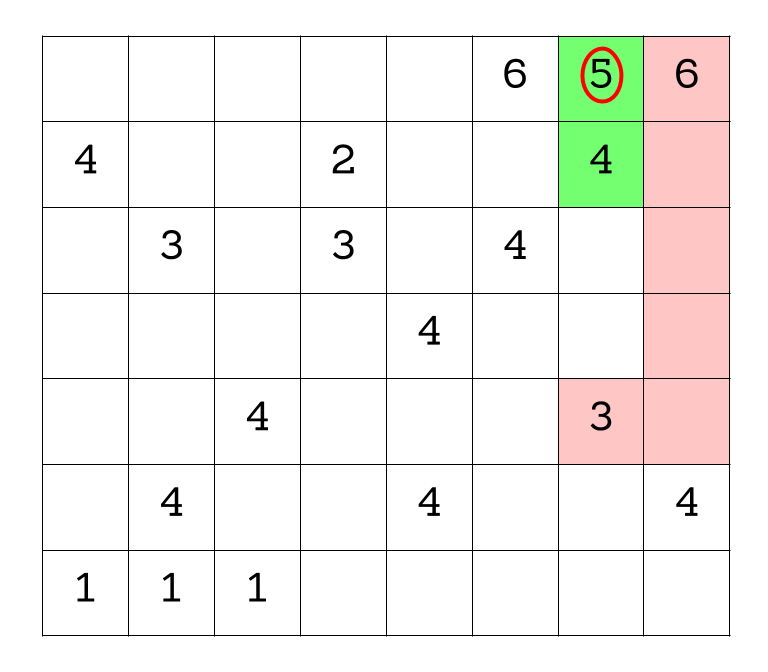
Now turning to the only 5 in the grid we know it must include the 4 immediately below it because that is the only direction we can expand this region without including a 6 and bumping our sum up to 11, which is too high.
Next I would like to tackle the 6 that is remaining but it is hard to figure out which 3 belongs in the same region as it since neither is too far away. So, let’s look at the 1’s. Because they are odd, each one has to be in its own region. And because they are adjacent, we have fewer directions we can go.
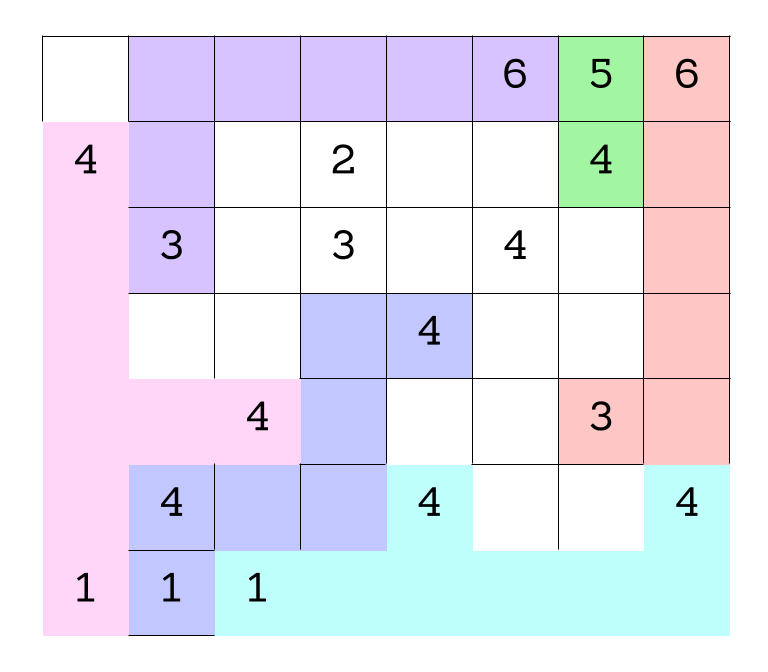
Starting with the 1 in the bottom lefthand corner, we know it has to include the two 4’s (indicated in the figure below). All the other even numbers are either too far away (shown in red) or if we included them in the new purple region we would cut off the other 1’s so that they would need to share a region, which we can’t do (we have highlighted those numbers in green). So, none of those numbers can be included in this region leaving only 2 available 4’s to be included in pink.
Moving on to the next 1 (circled in red) we see again most of the even numbers are too far away to be included in this blue region (in red). There is just one 4 that is close enough to work, but if we include it in blue the 1 that is leftover will be cut off from all but a single 4, which would not be a workable region. So, the green 4 can’t be included either, leaving us with the blue region shown below.
At this point you might be thinking,Wait! The green region has only two tiles, the pink region has 8, the salmon-colored region only has 6. Aren’t they all supposed to have 8 tiles in a region?
Well, that’s right, each region does need to have eight tiles in our final solution. But it is really hard to see how blank tiles should be assigned to make everything work out, so we will start by just figuring out which numbers should share a region, and then see if we can divvy up the blank tiles from there. That’s why our regions will each add up to 9 to start with, but they may not have 8 tiles in them just yet.
Now we just have one 1 left and two of the remaining even numbers (highlighted in red) are too far away. If we included the other 4 (highlighted in green) then we would end up cutting off the 4 in the bottom right corner. With just two of the 4’s left, we know that they should be included in the turquoise region below.
Now we can finally circle back to the remaining 6, and try to figure out which 3 it should be paired with. Now if we pair it with the right-most 3 (in green) we will cut off the remaining 4 from all the other numbers, which isn’t allowed. That leaves the 3 on the left, which we will include in the purple region.
The last numbers standing 2,3, and 4 of course must share a region. But now that we know which numbers share a region, let’s move on to expanding regions to have exactly 8 squares.
Two of the regions are already exactly 8 squares (pink and turquoise).
Now the only region the top left square can be included in is the purple region, which brings the purple region to a full 8 squares.
Now that the pink and purple regions are more settled we can tackle the last three numbers. We know they have to share a region (grey). The square outlined in red also has to be grey because if it was part of the blue region, then the blank square to the left of it would be cut off and couldn’t be added to any of the regions next to it.
With the four grey squares above filled in, we can complete the grey area, since all the blank squares to the left of the grey area have to be filled in grey and the 4 in grey has to be included in the grey region.
The green region must expand into the blank squares to the right and then down to keep it a single region of exactly 8 squares.
And with that we can complete the final region (salmon colored). Whew! What a process!?!
A few more questions
Now we can verify that this solution is indeed a solution, just by checking that each region does sum to 9 and each region does have exactly 8 squares. But another question you may be asking yourself, and what a mathematician might ask themselves about a solution like this, would be:
Is this the only solution (i.e. is it unique)? If it is the only solution, how could you show that it is the only one?
If you enjoyed solving this problem, you can tackle the additional questions above for some bonus fun. :)
Jayden’s Solution, BEAM Discovery 2020
This problem comes from USAMTS, a national math contest.