...And Now for Some Math

To recap from the newsletter:

You are eating a special candy bar. You and a friend each take turns eating squares of blue, pink, and green candy starting from the left and moving right. You can bite off as many squares as you want, so long as they’re all the same color of candy. So, for example, your first move could be to bite off 1, 2, 3, or 4 squares. The winner is the person who eats the green square of candy (which is extra delicious!).

Start by playing around with it and learning how it works. Then, start asking yourself some questions. Can you figure out how to win the game every time you play? Do you want to go first or second to try to win? Can you figure out how to find a winning strategy even if we changed the board you’re playing on?

The Solution

If you start from the beginning, this problem is a mess: there are lots of possibilities to consider. In fact, in our weekend class “Entry to Abstract Math,” this problem was used specifically to introduce the idea of working backwards from the end. Once you have that insight, it becomes quite easy!

Of course, immediately before the final bite, this will be what remains of the candy bar:

You want your opponent to leave you with just that green square. How can you guarantee that? Well, if your opponent is faced with this board, then they have no choice but to leave you with that delicious final square!

Now, if your goal is to leave your opponent with this board, then you want to eat the square right before it, so we’ll put a little bite symbol on the squares you should bite.

To make sure you have the chance to bite that square, you must leave your opponent with just one square before it so they have no choice but to leave you with this configuration:

Which means you want to bite the square right before it:

This time, though, to make sure you can bite that marked pink bite, you need your opponent to leave you with all three pink squares. Otherwise, your opponent could bite to the pink bite and leave you in a losing position!

So how are you guaranteed to get all three pink squares? Simple, you must leave your opponent with just the single square before the pink region:

To guarantee that, you need to bite immediately to the left of that blue square:

If you want to be guaranteed that bite, your opponent must leave you with both pink squares. Otherwise, they could eat both! So you must leave them with just the one square before:

Which means you must bite the square immediately before it, which you can do on the first move:

Thus, the winning strategy is to go first, and bite up to each mark on your turn. If you go first, you will always be able to bite up to a mark (and your opponent will not!)

In addition to teaching about working backwards, this problem helps to introduce the ideas behind combinatorial game theory. In combinatorial game theory, not just can you analyze winning positions in games and develop winning strategies, but you can also develop a theory that lets you assign to each game a certain value that encodes how it works. These values (they’re not quite numbers) can be added together, and in fact, games can be added together as well in a compatible way!

In other words, this problem, which is already fun, is just the beginning!

—

Thanks to Mira Bernstein for creating and sharing this problem.

... And Now for Some Math

Try your hand at a Problem of the Week from BEAM Discovery (our summer program for rising 7th graders)! The Problem of the Week gives students a chance to explore interesting math outside of their classes, either on their own or in collaboration with others. It also provides an opportunity to build relationships with site leadership (who usually grade the problems), and a chance for staff to celebrate persistence in problem solving. This summer, students who solved a Problem of the Week received a special badge. See if you can solve Week 4’s Problem of the Week!

Solution:

One of the BEAM Discovery students who solved this problem was Jayden. You can see his submission at the end of this post!

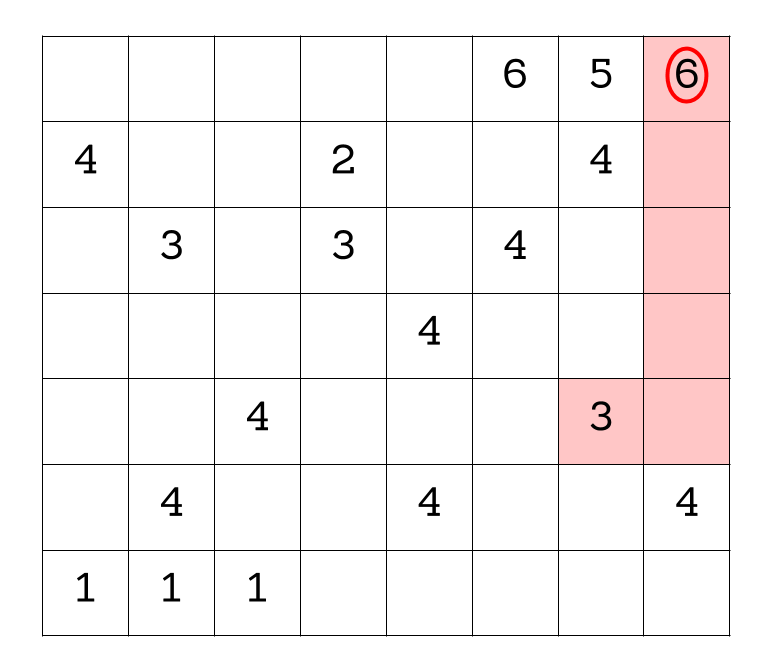
There are 56 squares in the grid, which has to also be equal to the number of regions times the number of squares in each region. Meanwhile, the sum of the numbers is 63, which has to also be equal to the number of regions times the sum in each region. This is where we can combine two facts to make the problem simpler: the number of regions must divide both 56 and 63! Since the only common divisors are 1 and 7 (and one region doesn't solve the problem), there must be 7 regions. Dividing, we see that each region has 56/7=8 squares, and the sum in each region is 63/7=9.

Now that we are satisfied that the only possible solution will have 7 regions with 8 squares in each region and each region should sum to 9, we still have the very tricky task of figuring out if we can actually come up with such a configuration. This seems like a pretty daunting task. One way to make it a little easier is to start with the squares containing large numbers (like 5 or 6) since there might be more limited options for the regions that contain them.

It also helps to lay out a couple of “rules” that help guide how we can build regions.

1. A number can’t be paired with a number that is “too far away.” Too far away means that it would take too many blocks to include it in the part of the region that is already determined, since each region can only be 8 blocks in total. For example, the 6 in the top right can’t be in the same region as the 1 in the bottom left, because it would take too many blocks to connect them.

2. Each region must contain exactly one odd number. Why? Because each region has to sum to 9, which is an odd number; therefore, it must contain at least 1 odd number. But there are exactly 7 odd numbers in total on the grid, so none of the 7 regions can contain more than one.

Just a note: To save time on the explanation, we're going to make a few simplifying guesses, but it is possible to solve the entire puzzle without having to make any guesses about how things come out!

First let’s think about the two 6’s, because those seem like they might be the easiest. Because the 6’s are the biggest numbers in the grid, and they can’t be paired with any 4’s or 5’s, this helps immediately narrow down our options. They also can’t be paired with any of the 1’s, according to rule 1, since the 1’s are too far away.

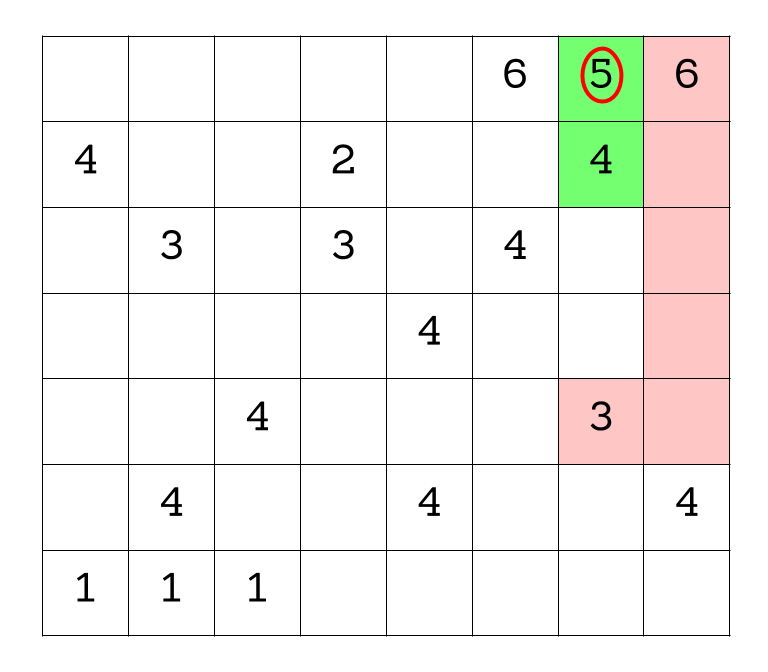
Starting with the 6 in the upper righthand corner, there is only one 3 available to be included in this region, as all the other 3’s are too far away/we would need to include another number in the region which would make it to have too high of a sum.

Now turning to the only 5 in the grid we know it must include the 4 immediately below it because that is the only direction we can expand this region without including a 6 and bumping our sum up to 11, which is too high.

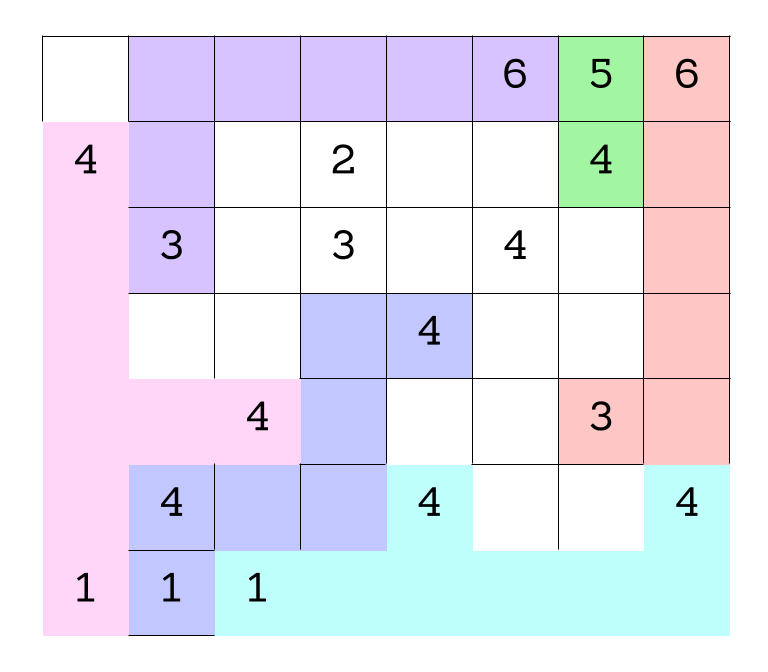
Next I would like to tackle the 6 that is remaining but it is hard to figure out which 3 belongs in the same region as it since neither is too far away. So, let’s look at the 1’s. Because they are odd, each one has to be in its own region. And because they are adjacent, we have fewer directions we can go.

Starting with the 1 in the bottom lefthand corner, we know it has to include the two 4’s (indicated in the figure below). All the other even numbers are either too far away (shown in red) or if we included them in the new purple region we would cut off the other 1’s so that they would need to share a region, which we can’t do (we have highlighted those numbers in green). So, none of those numbers can be included in this region leaving only 2 available 4’s to be included in pink.

Moving on to the next 1 (circled in red) we see again most of the even numbers are too far away to be included in this blue region (in red). There is just one 4 that is close enough to work, but if we include it in blue the 1 that is leftover will be cut off from all but a single 4, which would not be a workable region. So, the green 4 can’t be included either, leaving us with the blue region shown below.

At this point you might be thinking,Wait! The green region has only two tiles, the pink region has 8, the salmon-colored region only has 6. Aren’t they all supposed to have 8 tiles in a region?

Well, that’s right, each region does need to have eight tiles in our final solution. But it is really hard to see how blank tiles should be assigned to make everything work out, so we will start by just figuring out which numbers should share a region, and then see if we can divvy up the blank tiles from there. That’s why our regions will each add up to 9 to start with, but they may not have 8 tiles in them just yet.

Now we just have one 1 left and two of the remaining even numbers (highlighted in red) are too far away. If we included the other 4 (highlighted in green) then we would end up cutting off the 4 in the bottom right corner. With just two of the 4’s left, we know that they should be included in the turquoise region below.

Now we can finally circle back to the remaining 6, and try to figure out which 3 it should be paired with. Now if we pair it with the right-most 3 (in green) we will cut off the remaining 4 from all the other numbers, which isn’t allowed. That leaves the 3 on the left, which we will include in the purple region.

The last numbers standing 2,3, and 4 of course must share a region. But now that we know which numbers share a region, let’s move on to expanding regions to have exactly 8 squares.

Two of the regions are already exactly 8 squares (pink and turquoise).

Now the only region the top left square can be included in is the purple region, which brings the purple region to a full 8 squares.

Now that the pink and purple regions are more settled we can tackle the last three numbers. We know they have to share a region (grey). The square outlined in red also has to be grey because if it was part of the blue region, then the blank square to the left of it would be cut off and couldn’t be added to any of the regions next to it.

With the four grey squares above filled in, we can complete the grey area, since all the blank squares to the left of the grey area have to be filled in grey and the 4 in grey has to be included in the grey region.

The green region must expand into the blank squares to the right and then down to keep it a single region of exactly 8 squares.

And with that we can complete the final region (salmon colored). Whew! What a process!?!

A few more questions

Now we can verify that this solution is indeed a solution, just by checking that each region does sum to 9 and each region does have exactly 8 squares. But another question you may be asking yourself, and what a mathematician might ask themselves about a solution like this, would be:

Is this the only solution (i.e. is it unique)? If it is the only solution, how could you show that it is the only one?

If you enjoyed solving this problem, you can tackle the additional questions above for some bonus fun. :)

Jayden’s Solution, BEAM Discovery 2020

This problem comes from USAMTS, a national math contest.

... And Now for Some Math

This was a Challenge Problem last summer at our Bard College site. Challenge Problems encourage students to work collaboratively; once it's solved, the whole program gets a prize. (For this one, a sleepover on the last night!) So now it's your turn... can you solve it?

Malachi takes 42 pieces of candy, each of which is either a Skittles or an M&M, and arranges them in a circle letter side down (so they look identical!). He tells Hodaya that 23 of the candies are next to at least one Skittles, and 35 are next to at least one M&M. If Hodaya can figure out how many Skittles and how many M&Ms there are, she gets all of them!

How can Hodaya figure this out? (The answer appears below the image.)

Solution:

The important thing is to go step-by-step to figure out what you can.

If there are 23 candies next to at least one Skittles, that means 42-23=19 candies are not next to any Skittles — so they must be next to two M&Ms.

If 19 candies are next to two M&Ms and 35 are next to at least one M&M, that means 35-19=16 are next to exactly one M&M.

Now here's the key insight. Suppose there are x M&M's. Each M&M has a neighbor on the left and on the right, so if you add up for all the pieces how many M&M neighbors they have, you should get 2x. Well, we know that 19 candies are next to two M&Ms, so they have a total of 38 M&M neighbors. And 16 are next to one M&M, so they have 16 M&M neighbors. That gives 54 total M&M neighbors.

Divide by two to get 54/2=27 M&Ms in total.

With 42 candies in total, subtract out the M&Ms to get 42-17=15 Skittles.

Sometimes, it's amazing how much you can figure out with what seems like too little information!

How would you do at a BEAM trivia night?

What does it look like to combine puzzles, trivia, and a bit of math? BEAM's Slightly-Mathy Trivia Nights do just that, challenging guests to work together with students on fun, weird, challenging puzzles. If you want a taste of what that means, here are four rounds from our 2018 event. Scroll carefully as we’ve included the problems and then the answers on a next page. (Warning: Round 4 is hard!)

For Round 1, answer these questions first, and then click on the Round 1 link below to match each answer with a mathy symbol or drawing for double points!

1. What ocean borders on the US, Canada, Russia, Greenland, and Norway—but not Ghana or Namibia?

2. What is the last name of a famous tennis player whose first name is Bjorn?

3. What is the word for an old leather or metal glove?

4. What word means “placed more bullets into my gun”?

5. What public company has the highest market capitalization?

6. What programming language that is a dialect of Lisp is also a word for a devious plan?

7. In baseball, a line blank is what happens when the batter hits the ball hard with a low arc. What word fits in for the blank?

Thanks to all the BEAM students, supporters, and staff who joined us for trivia nights in Los Angeles and New York. Please join us next year! Sign up for our mailing list to get announcements about events in 2019.

4 for 15: An hour of class at BEAM 6 Uptown

This month, we're welcoming three new full-time staff to BEAM! One of them, Alyssa Loving Jung, is BEAM's new Development and Communications Coordinator. She spent her first week at BEAM visiting BEAM 6 and wrote this blog post about her experience. Welcome to the team, Alyssa!

----

My goal is to sit in on four of BEAM 6 Uptownʻs math classes in a single hour. While I may have an advanced degree in mathematics (a Master's to be precise), it is an ambitious plan. I am eager to see what mathematics the BEAM 6 students will be tackling today. 

----

To start off, I get to join the very beginning of a class that appears to be about exponents… or maybe number theory? I am not quite sure. On the board there is a question that immediately catches my eye. 

What is the ones digit of 569,423^22?

I can't help it. I immediately start scribbling work in my notebook trying to solve the question. But as discussion swirls around me, I am pulled away from my attempts to solve the problem, curious as to what the students are coming up with. Students wonder out loud how to deal with a problem like this without doing a dizzying degree of multiplication. The instructor, Juan, offers a friendly warning that such an approach would take much more time than they have in class. Returning to my page of notes, I gather from my own work that the key to the problem lies in spotting a pattern and not getting lost in the cumbersome calculations. 

Emily works during class. 

Around me, I can hear students closing in on the pattern, and it is such fun that I must force myself to remember that I only have 15 minutes at most with them before I have to head to the next class. 

Even before my time is up, one of the students is up at the board presenting an idea.  

Collaborative mathematics, the courage to expose a budding solution, a still green idea, to an entire class of peers, is a crucial element of pursuing advanced mathematics. I am delighted that BEAM students are engaging with each other and their faculty like this. But glancing at the clock, I must tear myself away and head to the next class. 

----

Here there is a very different sort of picture on the board. 

There are intersecting circles drawn and numbers scattered about. A student is at the board placing a number with care. While the numbers seem haphazardly distributed at first, the thoughtfulness of the student is the first clue that something more is going on. Then I notice the labels: factors of 6, multiples of 6, primes. 

They are exploring logic. The strange picture on the board I recognize as a Venn Diagram, a way to visualize the overlap and interplay between different sets. 

They move on from the Venn Diagram on the board to start working on a sheet of problems. A student notices ambiguity in one of the problems. The problem asks them to explore the statement "not A or B". He wonders if the instructor, Sian, means "(not A) or B" or rather "not (A or B)". 

The whole class takes time to investigate this subtlety. The process reminds me of writing math proofs during graduate school. Oftentimes the tiniest turn of phrase, the most minute missing detail, can make or break a complex mathematical argument. I am excited to see that the students are taking such care with the reading and writing of mathematics. But it is time for me to move on to my third class. 

TA Amaya works with student Karen on a problem set during Open Math Time.

----

Yorlan works on an advanced geoemetry problem. 

This class says Geometry and Logic in the corner of the chalkboard at the front. Apparently, it is another class on logic, but now there is geometry thrown into the mix. I am intrigued. 

The instructor, Xavier, is energetic and he calls each student by name as he peppers the room with questions. 

He wonders how we can figure out what c is when we know c^2=8. A student calls out that c is the square root of 8.

Xavier follows up, smiling, to see if Eduardo was just guessing, but no: 

"No, I didn’t guess..." Eduardo responds, "It's 'cause taking the square root is the opposite of squaring something." 

I am impressed that in one sentence Eduardo has gotten at the heart of what mathematicians mean by inverse equations. It is a concept that can confound even college students. But I can’t stay for more insights today. 

----

I am off to my final class. As I slip into my seat, I am startled to see scrawled across the board: "Are there Aliens in the Milky Way?" 

A massive equation containing many letters is sprawled somewhere beneath it. The students are clearly in the process of grappling with the equation and what it means. The instructor, Susan, asks them to replace L = (1/10)^8 in their previous calculation, with L = (1/10)^2. Immediately, diligent pencil-scratching begins, heads bent, eyebrows furrowed with concentration. 

This is what I call the "dirty work" of mathematics. Complex computations don’t encompass what mathematicians do. Mathematicians are much more than mere human calculators after all. But such calculations do form an important aspect of the job of many mathematicians and scientists. BEAM students in this class are building the patience and the stamina to handle even very complex formulas, and learning some mind-boggling astronomy at the same time. 

Taro, a TA, observes Jamal as he contemplates a large numbers. 

Meanwhile, I have set a new personal record for how many classes I have attended in one hour, and better yet I have had the chance to think about some really cool math. I cannot wait for what the next hour of BEAM 6 has in store!

----

Curious about the classes that Alyssa visited? BEAM 6 students all take classes in our four topic areas: Math Fundamentals, Logic, Math Team Strategies, and Applied Math. Within each topic, students get to choose from a menu of classes, so they each take a class that inspires their curiosity. In the mornings, when Alyssa was visiting classes, students were in either their Math Fundamentals class, which explores the why of elementary math, or Logic class, which focuses on how to justify your reasoning. Juan and Susan were each teaching Math Fundamentals courses, while Sian and Xavier teach courses in the Logic track. 

Here are the full course descriptions for the four classes she visited!

Exponents: The Super-Powers of Numbers! (Juan) 

Using the power of multiplication, we will build some really, really big numbers and compare them to see which ones will turn out to be the biggest. We'll also explore a strange planet which only has 11 numbers in it!

Cryptarithms and Other Arithmetic Puzzles (Sian)

If A + B = AC, then what is A + B + C?  Cryptarithms are math puzzles where the arithmetic is simple but the "thinking part" of the puzzle is challenging.  We will start with simple problems and build up a tool chest of logic strategies for solving these problems and all math problems.

Geometry and Logic (Xavier)

Ever look at a problem and not know where to start? This class will develop your ability to solve complex problems. We will learn how seemingly incomplete information can be combined to form complete solutions.

Big numbers, Small numbers, and In between (Susan)

Imagine you have a very long number line, with every number you’ve discussed this year in school on the number line. A new number is introduced. Where does it go? Are you sure? In this class, we will use a variety of tools (brain power, rulers, logic, and more) to identify the big numbers, the small numbers, and the ones in between.

Spotlight on Classes: Analytic Number Theory

Each week, the students are able to list their preferences for which classes they would like to take. They take one course for four hours a day, and another for two hours a day. Each week, new classes are offered and the students have the opportunity to immerse themselves in different advanced mathematical topics.

While each of BEAM’s classes explores incredibly interesting and advanced ideas, we’ve put together a spotlight on just one of the six courses offered this week: Analytic Number Theory with Cory. 

The class has just seven students, with a teacher and a teaching assistant—the kids get to really get to know one another and the staff members! In just three days, the class has gone from not knowing what a function is to being able to find the limit as n approaches infinity of f(n) = (-1)n/n: zero. The students are basically doing calculus without using the word “calculus” itself! 

Sitting in on the class, what is most impressive to our staff, even more than the sheer speed and intensity of the class, is how engaged each student is. Cory will give short lectures, but for a majority of the class, the students work in small groups in order to work on difficult problem sets. Mostly, they are teaching themselves the topics! Today in class, we were beyond impressed to see how each of the students was able to find patterns and draw conclusions from sequences of numbers.

When Anaís and Cynthia talked about the class, they said that they couldn’t believe how much they were learning in such a short period of time!

Jack agreed, saying: “I’ve learned more math in the past three days than I did in the last two months.” 

Cynthia, Jack, Anaís, and Alvin work together on the board

Week two classes are now officially over at BEAM 7 Union College. We can't wait to see how much learning takes place in week three!

Welcome to BEAM 6 2017

Week 1: Start of Something New

The summer is in full swing, but BEAM is just getting started. So far students have been assorted into one of two sets, either Calderón or Granville, and begun taking classes in Logical Reasoning, Math Fundamentals, Applied Math, and Math Team Strategies.

Faculty member David assists Justin, Jose, and Conaré during Open Math Time. 

Some students are excited about taking their first class on computer programing, while others are asking hard hitting questions about force and relativity in their Space class.

"Give me more challenging problems" -Lilly (Calderón) proudly displaying her decorated binder

Jason, Brianna, Messiah, and Mohammad are enjoying an exciting game of Kickball. 

Open Math Time (OMT) gave everyone a chance to work on problem sets in groups or ask for assistance from the Teaching Assistants.

Nicole, Maryam, and Aamirah working during OMT

Last week many students have attempted this week's challenge problem during their OMT. Ten students have already completed the Challenge Problem. Students are discovering they have a lot in common with kids from both sets during their daily and weekly activity times.

What's happened in the first week at Bard?

First things first. Where exactly is Bard? Located about about a 2 hour drive north of New York City, our site for BEAM 7 rests right along the Hudson River nestled among the trees. While at Bard, BEAM7 operates most heavily in three buildings: Keene, our home base and dormitory for students and staff; Kline, the cafeteria where we eat all three meals each day; and Hegeman, where most activities and classes take place!

 

---

Activities!

Pictured above: Counselor Kaylynn (middle) and instructor Javier (left of Kaylynn) play Set, a matching game which requires players to recognize patterns in a set of cards, with students Jack, Storm, and Seb. 

At BEAM, students get to choose between a variety of activities offered by counselors and faculty, ranging from high-energy sports and games to more relaxing crafts. So far this week, counselors have run:

• Soccer, Ultimate Frisbee, Capture the Flag, Basketball
• Mandala Coloring, Hexaflexagon Making, Paper Airplanes
• THE Egg Drop Contest
• Cloud Watching, Exploring Bard's Campus, Settles of Catan

And this is just throughout the first week! Over the next two weeks, the counselors and staff will have many more activities to come...

---

But what about the math?

A number of students work diligently on problem sets in their Math Team Strategies class, which reviews techniques for quick in easy problem solving in the face of seemingly difficult questions. Mathematicians can be a lazy bunch, so learning the techniques to making challenging problems easier is an important skill set!

So what math are the kids actually doing? This week, we have the following options:

• Number Theory
• Combinatorics
• Turing Machines
• Graph Theory
• Math Team Strategies
• Solving Big Problems

The best thing about our courses--besides the amazing instructors who design and teach them--students choose what interests them! Each student is in one of the first four options (called the core topics courses) and one of the last two options (called the problem solving courses). Stay tuned for more updates on what's happening at Bard for BEAM 7 2017!

"End of the Year" BEAM Spring Party 2017

Each year, BEAM invites all of their alumni to come together and celebrate the end of a successful school year. It's always great to see our alumni, play board games with them, and celebrate their accomplishments!

This year we added some cool stuff to our Spring partying! We had the return of the photo booth, some fun math puzzles (with prizes for those who completed them), a modular origami station, food including amazing Jollof rice made by Chuka's mother, and some piano playing. 

Modular Origami

Board Games

Photo Booth

Math puzzles

We even had time to show off some of our talents. Pictured here is Mariam (8th grader) singing and Laura (BEAM staff member) playing the piano. Needless to say, we had an amazing time!

Waking Up At BEAM

On Sunday, the BEAMers had woken up to the hustle and bustle of the city, but this Monday morning, they woke up to the country side’s silence.

After a pleasant walk to the dining hall through the ivy-covered and tree-filled campus, the students had breakfast, boosting their brains for the following Opening Challenge Set, a test designed to measure where the students are at in math. After completing the test, the BEAMers were taken outside, where icebreakers took place, even though the ice had broken a long time ago. Lunch followed, and then the students split up into their respective halls (Hopper, Noether, Ramanujan, and Euler) and received a step-by-step orientation on everything from their daily schedule to how to do laundry. Additionally, each student opened an Art of Problem Solving account as well. The BEAMers were then split up into the activities they had signed up for the night before, these being charades, soccer, a tour of the campus, and Fluxx (a card game). Afterwards, the BEAM instructors gave presentations on the courses they would be teaching this upcoming week, and the students filled out sheets with their preferences regarding the courses.

Later in the evening, while the instructors hid out, huddled together for hours, making sure every student was placed in the appropriate course, the BEAMers enjoyed free time back at the dorms and the basketball court. Hall meetings were held before bed, and the students would wake up tomorrow to their first day of class and to find out what course they’d been assigned to for the upcoming week. What a day for the BEAMers to look forward to.