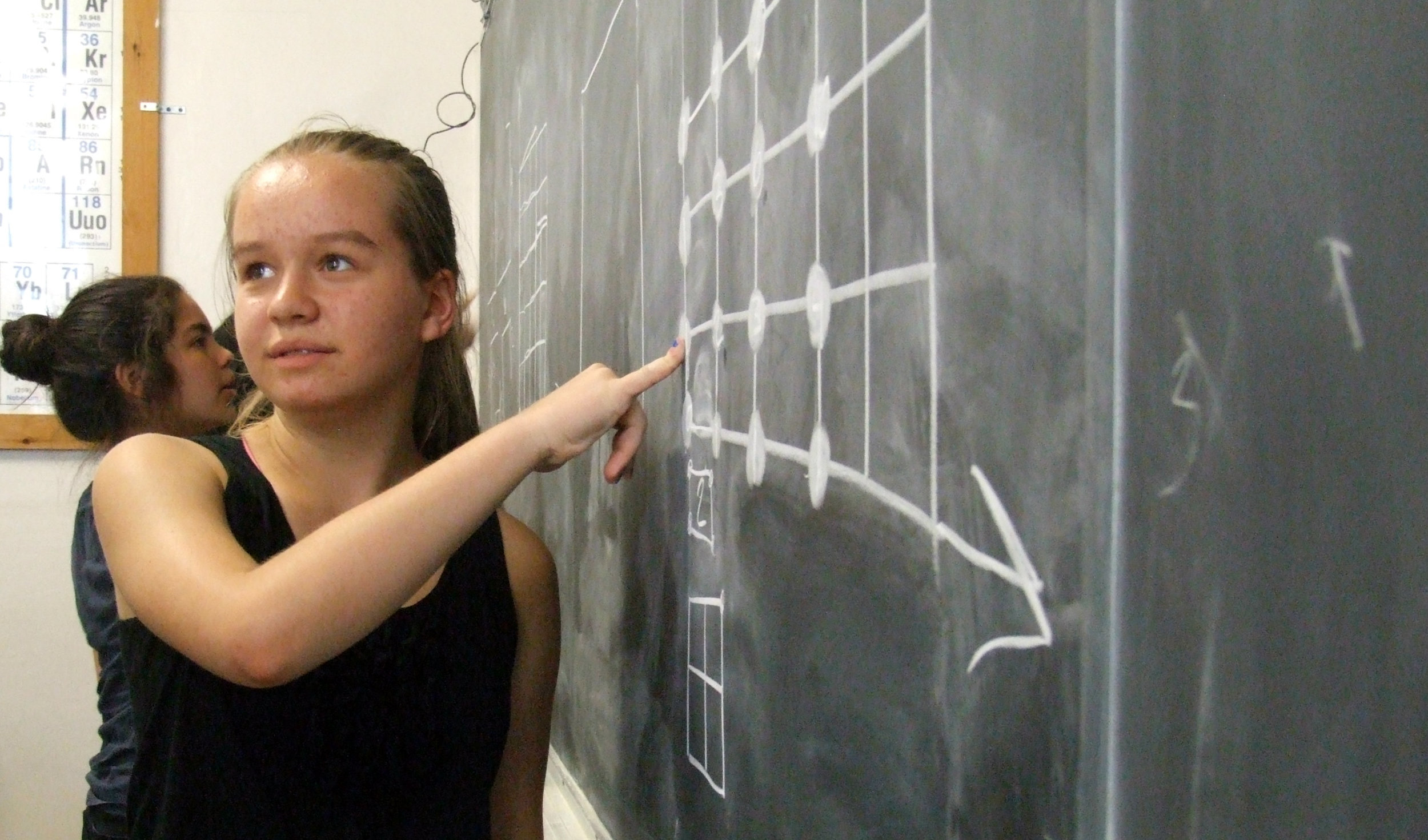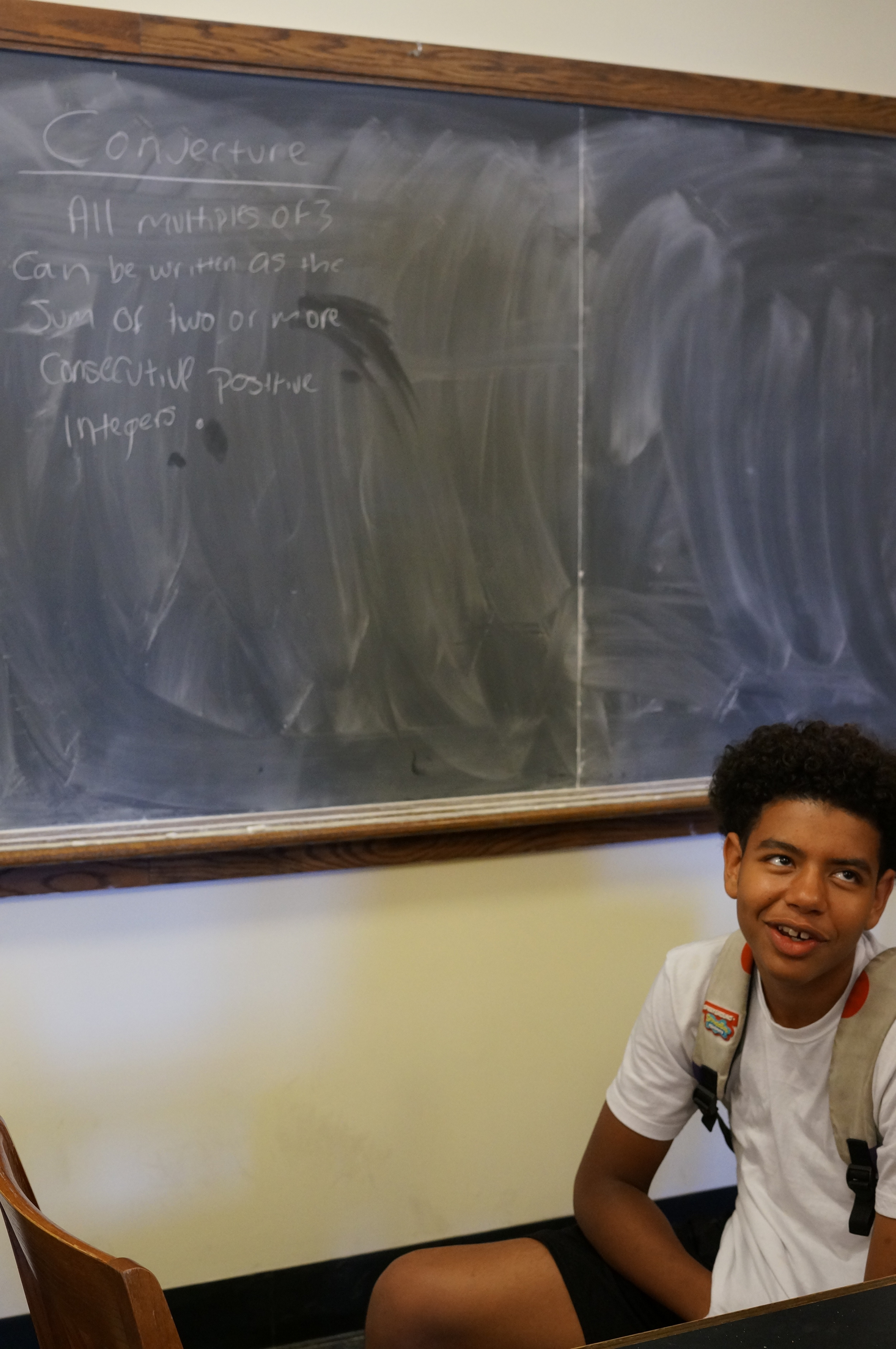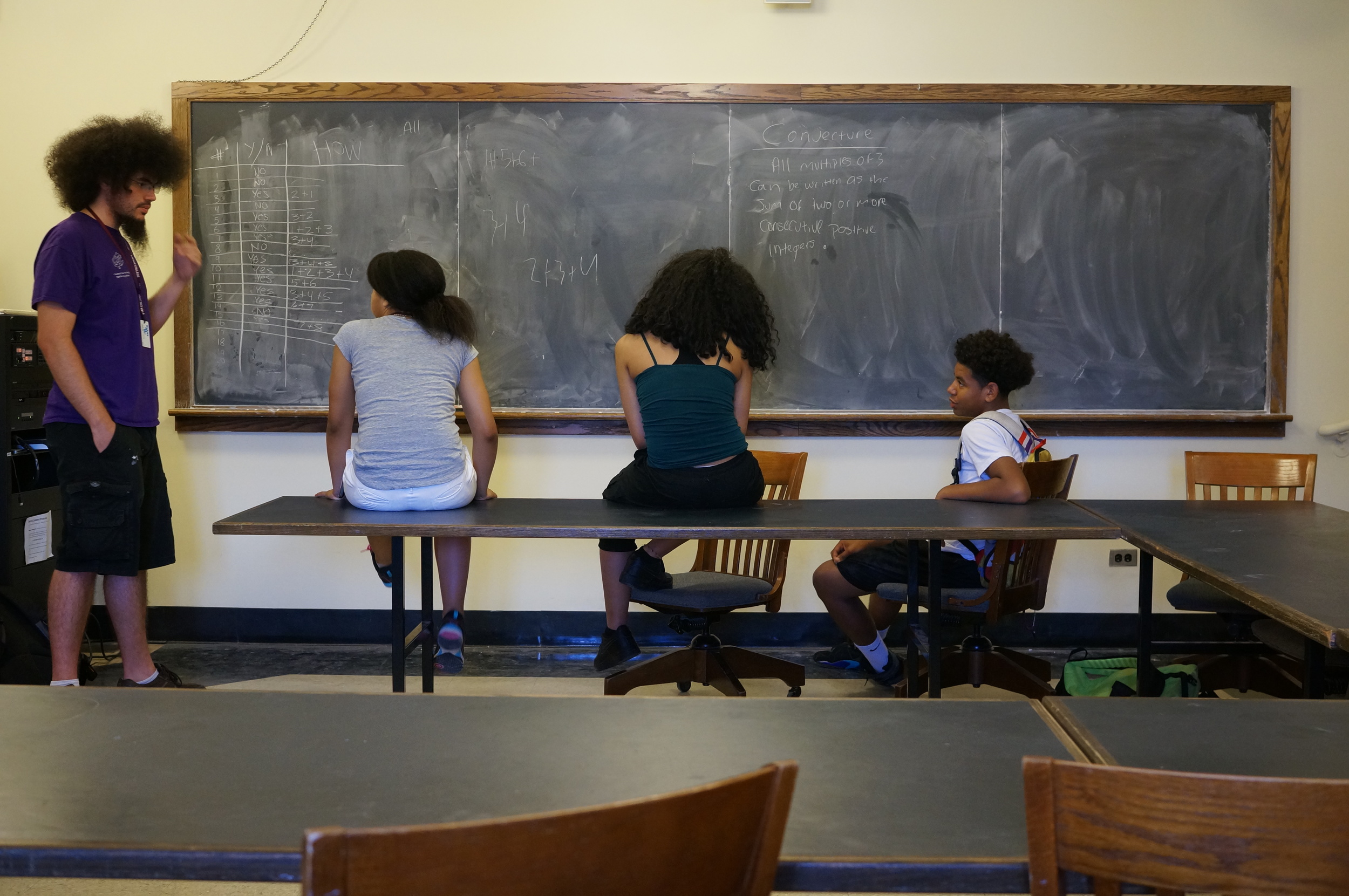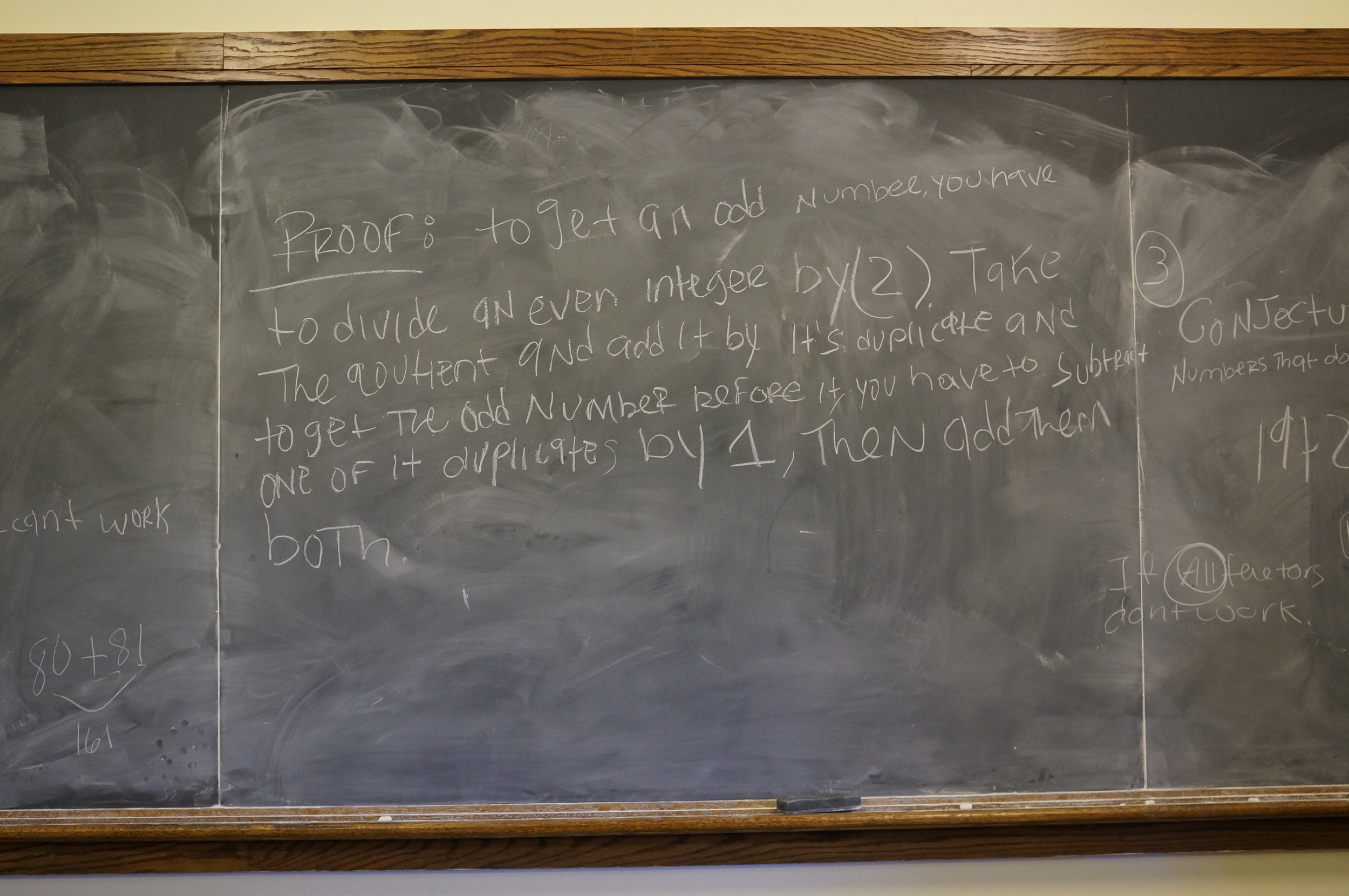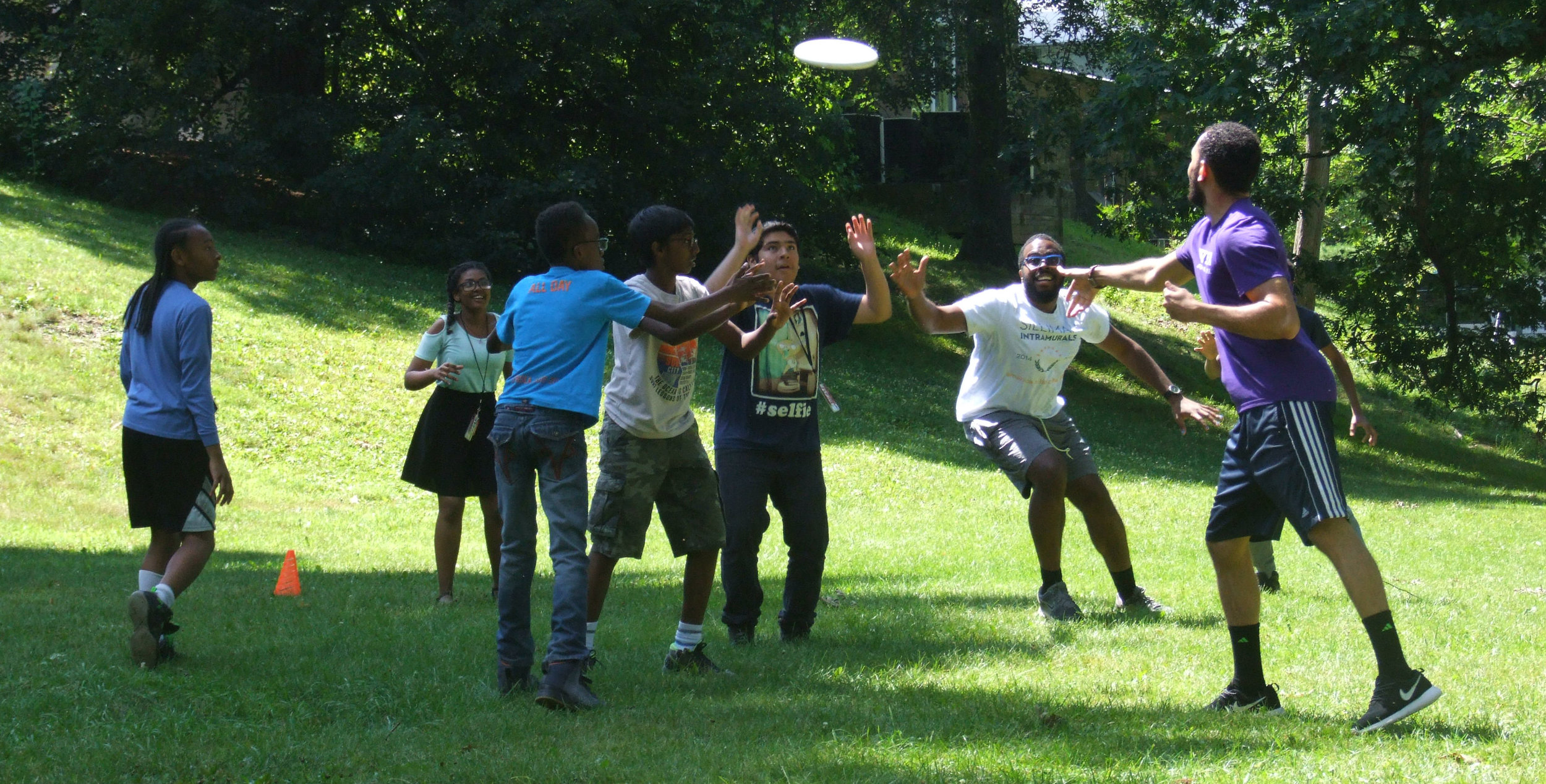A Day at BEAM Discovery

So what exactly happens at BEAM Discovery? Here’s a look at a typical day, featuring photos from BEAM Discovery’s Downtown NYC campus!

The morning starts with breakfast, followed by morning classes. BEAM believes in choice, so students pick classes, which might be “Beating Sherlock” or “Fractions, Puzzles, and Games.”

After class, students have an hour of Open Math Time, time where they can work on any math they choose, individually or in groups. They make sure to complete required PSets (problem sets) from class, and they can then explore challenges (the Problem of the Week or the 100 Problem Challenge), math books, coding websites, the Art of Problem Solving, and more.

After class, it’s on to activities! BEAM students get their choice of sports, board games, arts and crafts, and other creative activities. Recent hits included how to solve a Rubik’s cube, origami, anime club, and relay tic-tac-toe.

After activities, it’s off to lunch. BEAM pays for catered lunch from local restaurants every day. These photos are from empanada Thursday!

Most days, the afternoon block features an exact repeat of the morning block: class, open math time, activities. But one day each week, we have special afternoons, which feature Relays, a team-based math competition where students solve math challenges with some silliness mixed in. A recent problem required students to hum a tune their judge would recognize before they gave their math answer!

When the day wraps up, students join their travel groups to take the subway home and relax and recharge so their brains are fresh for another day at BEAM!

4 for 15: An hour of class at BEAM 6 Uptown

This month, we're welcoming three new full-time staff to BEAM! One of them, Alyssa Loving Jung, is BEAM's new Development and Communications Coordinator. She spent her first week at BEAM visiting BEAM 6 and wrote this blog post about her experience. Welcome to the team, Alyssa!

----

My goal is to sit in on four of BEAM 6 Uptownʻs math classes in a single hour. While I may have an advanced degree in mathematics (a Master's to be precise), it is an ambitious plan. I am eager to see what mathematics the BEAM 6 students will be tackling today. 

----

To start off, I get to join the very beginning of a class that appears to be about exponents… or maybe number theory? I am not quite sure. On the board there is a question that immediately catches my eye. 

What is the ones digit of 569,423^22?

I can't help it. I immediately start scribbling work in my notebook trying to solve the question. But as discussion swirls around me, I am pulled away from my attempts to solve the problem, curious as to what the students are coming up with. Students wonder out loud how to deal with a problem like this without doing a dizzying degree of multiplication. The instructor, Juan, offers a friendly warning that such an approach would take much more time than they have in class. Returning to my page of notes, I gather from my own work that the key to the problem lies in spotting a pattern and not getting lost in the cumbersome calculations. 

Emily works during class. 

Around me, I can hear students closing in on the pattern, and it is such fun that I must force myself to remember that I only have 15 minutes at most with them before I have to head to the next class. 

Even before my time is up, one of the students is up at the board presenting an idea.  

Collaborative mathematics, the courage to expose a budding solution, a still green idea, to an entire class of peers, is a crucial element of pursuing advanced mathematics. I am delighted that BEAM students are engaging with each other and their faculty like this. But glancing at the clock, I must tear myself away and head to the next class. 

----

Here there is a very different sort of picture on the board. 

There are intersecting circles drawn and numbers scattered about. A student is at the board placing a number with care. While the numbers seem haphazardly distributed at first, the thoughtfulness of the student is the first clue that something more is going on. Then I notice the labels: factors of 6, multiples of 6, primes. 

They are exploring logic. The strange picture on the board I recognize as a Venn Diagram, a way to visualize the overlap and interplay between different sets. 

They move on from the Venn Diagram on the board to start working on a sheet of problems. A student notices ambiguity in one of the problems. The problem asks them to explore the statement "not A or B". He wonders if the instructor, Sian, means "(not A) or B" or rather "not (A or B)". 

The whole class takes time to investigate this subtlety. The process reminds me of writing math proofs during graduate school. Oftentimes the tiniest turn of phrase, the most minute missing detail, can make or break a complex mathematical argument. I am excited to see that the students are taking such care with the reading and writing of mathematics. But it is time for me to move on to my third class. 

TA Amaya works with student Karen on a problem set during Open Math Time.

----

Yorlan works on an advanced geoemetry problem. 

This class says Geometry and Logic in the corner of the chalkboard at the front. Apparently, it is another class on logic, but now there is geometry thrown into the mix. I am intrigued. 

The instructor, Xavier, is energetic and he calls each student by name as he peppers the room with questions. 

He wonders how we can figure out what c is when we know c^2=8. A student calls out that c is the square root of 8.

Xavier follows up, smiling, to see if Eduardo was just guessing, but no: 

"No, I didn’t guess..." Eduardo responds, "It's 'cause taking the square root is the opposite of squaring something." 

I am impressed that in one sentence Eduardo has gotten at the heart of what mathematicians mean by inverse equations. It is a concept that can confound even college students. But I can’t stay for more insights today. 

----

I am off to my final class. As I slip into my seat, I am startled to see scrawled across the board: "Are there Aliens in the Milky Way?" 

A massive equation containing many letters is sprawled somewhere beneath it. The students are clearly in the process of grappling with the equation and what it means. The instructor, Susan, asks them to replace L = (1/10)^8 in their previous calculation, with L = (1/10)^2. Immediately, diligent pencil-scratching begins, heads bent, eyebrows furrowed with concentration. 

This is what I call the "dirty work" of mathematics. Complex computations don’t encompass what mathematicians do. Mathematicians are much more than mere human calculators after all. But such calculations do form an important aspect of the job of many mathematicians and scientists. BEAM students in this class are building the patience and the stamina to handle even very complex formulas, and learning some mind-boggling astronomy at the same time. 

Taro, a TA, observes Jamal as he contemplates a large numbers. 

Meanwhile, I have set a new personal record for how many classes I have attended in one hour, and better yet I have had the chance to think about some really cool math. I cannot wait for what the next hour of BEAM 6 has in store!

----

Curious about the classes that Alyssa visited? BEAM 6 students all take classes in our four topic areas: Math Fundamentals, Logic, Math Team Strategies, and Applied Math. Within each topic, students get to choose from a menu of classes, so they each take a class that inspires their curiosity. In the mornings, when Alyssa was visiting classes, students were in either their Math Fundamentals class, which explores the why of elementary math, or Logic class, which focuses on how to justify your reasoning. Juan and Susan were each teaching Math Fundamentals courses, while Sian and Xavier teach courses in the Logic track. 

Here are the full course descriptions for the four classes she visited!

Exponents: The Super-Powers of Numbers! (Juan) 

Using the power of multiplication, we will build some really, really big numbers and compare them to see which ones will turn out to be the biggest. We'll also explore a strange planet which only has 11 numbers in it!

Cryptarithms and Other Arithmetic Puzzles (Sian)

If A + B = AC, then what is A + B + C?  Cryptarithms are math puzzles where the arithmetic is simple but the "thinking part" of the puzzle is challenging.  We will start with simple problems and build up a tool chest of logic strategies for solving these problems and all math problems.

Geometry and Logic (Xavier)

Ever look at a problem and not know where to start? This class will develop your ability to solve complex problems. We will learn how seemingly incomplete information can be combined to form complete solutions.

Big numbers, Small numbers, and In between (Susan)

Imagine you have a very long number line, with every number you’ve discussed this year in school on the number line. A new number is introduced. Where does it go? Are you sure? In this class, we will use a variety of tools (brain power, rulers, logic, and more) to identify the big numbers, the small numbers, and the ones in between.

A Day in the Life of BEAM 6

It's Friday which means we are nearly 20% of the way finished with BEAM 6 Los Angeles 2018. Where did the time go??

So, what is a week like at BEAM 6? Each day features:

• Breakfast
• Morning class
• Open Math Time
• Activities
• Lunch
• Afternoon class
• Open Math Time
• Activities

Let's dig deep on each of those blocks! 

The day begins with a balanced breakfast, served a la carte in the cafeteria. 

Academics

Then, it's off to class!  Students at BEAM take four classes, one each in the following tracks: Logical Reasoning, Math Fundamentals, Math Team Strategies, and Applied Math. At the beginning of the summer, students selected which version of each class they wanted to take. Their options were:

• Logical Reasoning:
  • KenKen Puzzles and More
  • Ultimate Brain Puzzles!
  • Elementary, My Dear!
  • Liars, Truthtellers, and More
• Math Fundamentals:
  • Fractions and Food
  • Exponents: the Super-Powers of Numbers
  • Patterns, Lines, and Number Rules
• Applied Math:
  • Introduction to Cryptography
  • Voting: How to Run a Country
  • Computer Programming
• Math Team Strategies:
  • Using Patterns to Solve Problems
  • Counting Without Counting and Fantastic (Number) Beasts
  • Words, Meet Numbers: An Algebra Story

Don't those sound fun? How did students choose?? Each instructor gave a course description and a sample problem! Here's one set to consider!

Elementary, My Dear!

Course Description:

Ever wonder how detectives like Sherlock Holmes solve complicated mysteries? It's all in the details. In this class we'll explore the different techniques used to solve complicated riddles and how to apply them in tough mathematical problems.

Sample problem:

Mr. Red, Mr. Blue, and Mr. White meet at a restaurant for lunch. Under their coats they are wearing either a red, blue, or white shirt. Mr. Blue says, “Hey, did you notice we are all wearing different colored shirts from our names?” The man wearing the white shirt says, “Wow, Mr. Blue, that’s right.” Can you tell who is wearing what color shirt?

Open Math Time

One of the big goals of BEAM is that students spend time doing math they enjoy! So, during Open Math Time, students get a menu of options they can pursue. We encourage students to keep going back to this menu of options during 7th grade, whenever they're looking for a challenge!  During Open Math Time, students might:

• Reinforce learning from their classes with Problem Sets  
• Try out the weekly challenge problem
• Work on the 100 Problem Challenge (more on that later!)
• Explore the Art of Problem Solving, probably by checking out Alcumus

Students can work independently, or in groups!  It's really up to what makes each student the most productive. 

Activities

Morning activities last for the whole week! They're a time to learn new skills or spend a whole week on a passion. This week's options are:

• Board Games: Old classics and new! 
• Decorate Your Binder 
• Watch the World Cup: Watch live and old soccer games!  
• Learn to Solve A Rubik’s Cube
• Rooftop FUN: Steal The Bacon and Sharky Sharky 
• Learn to Play Settlers: A trading and building board game set in the mythical world of Catan!
• Learn Dominion: A strategy card game where each time you play it’s different! 

Afternoon

Then, it's on to lunch (buffet catering from local restaurants), the next class, the next block of Open Math Time, and afternoon activities, which change every day. 

All in all, it's a busy, exciting day, and we'll have much more to share over the upcoming weeks!

BEAMing Away

Weeks 1/2: Solving Big Problems

As mentioned earlier, all BEAM students study problem solving throughout the program.  Beyond Math Team Strategies, the other option is Solving Big Problems: working on the same problem for 2+ hours and really working to understand it.

In today's class, students investigated the following problem:

Which positive integers can be written as the sum of consecutive integers?

Students had a number of early conjectures, including:

• All odd integers have this property.
• If a given number is composed only of factors without this property, then that number also won't be possible to write as the sum of consecutive integers (so, if 4 = 1 * 2 * 2 and 1 and 2 are impossible, 4 is also impossible). 

The class was quickly able to prove the first conjecture, and then spent the next 2 hours working on the second.  Can you figure it out?

BEAMing Snippets