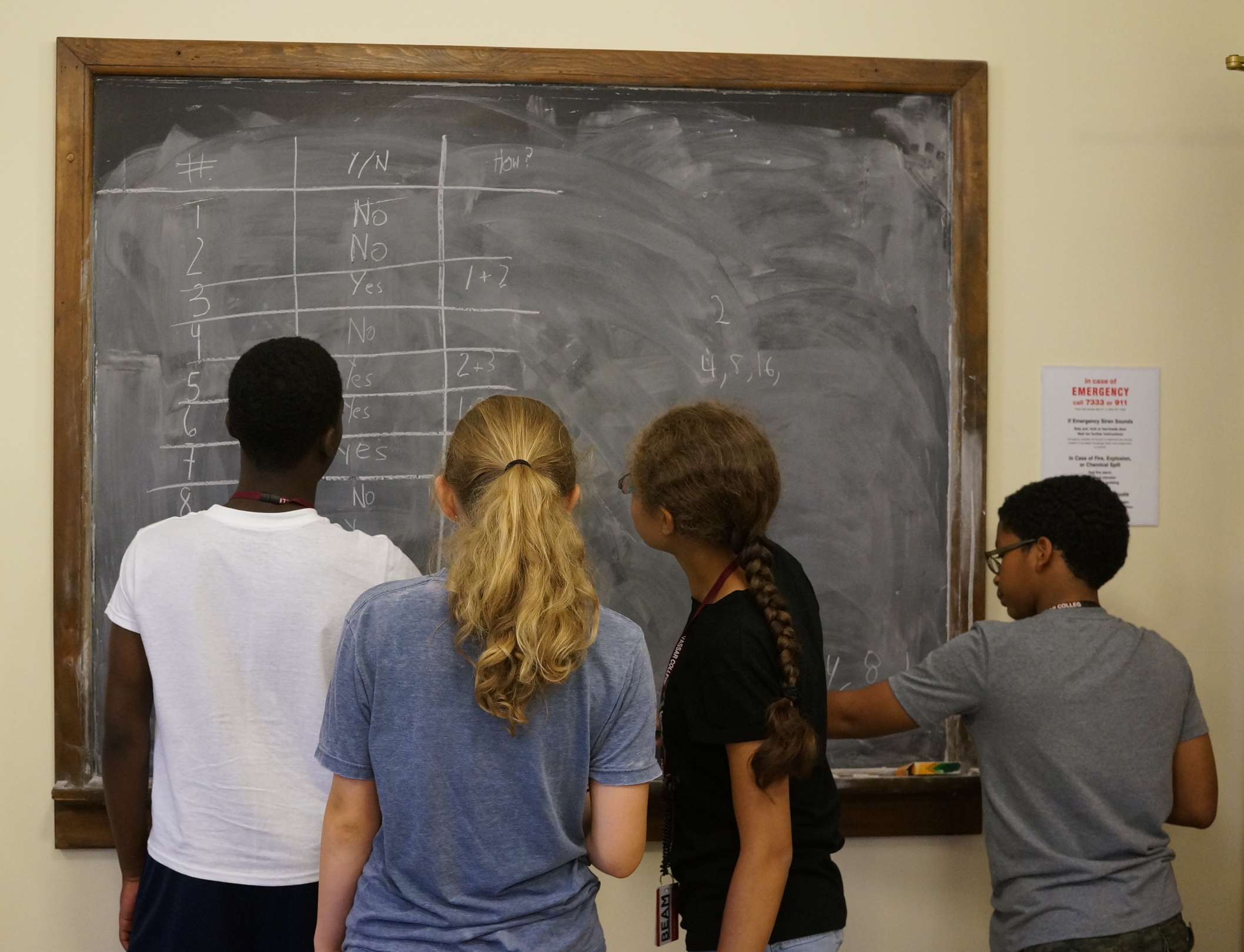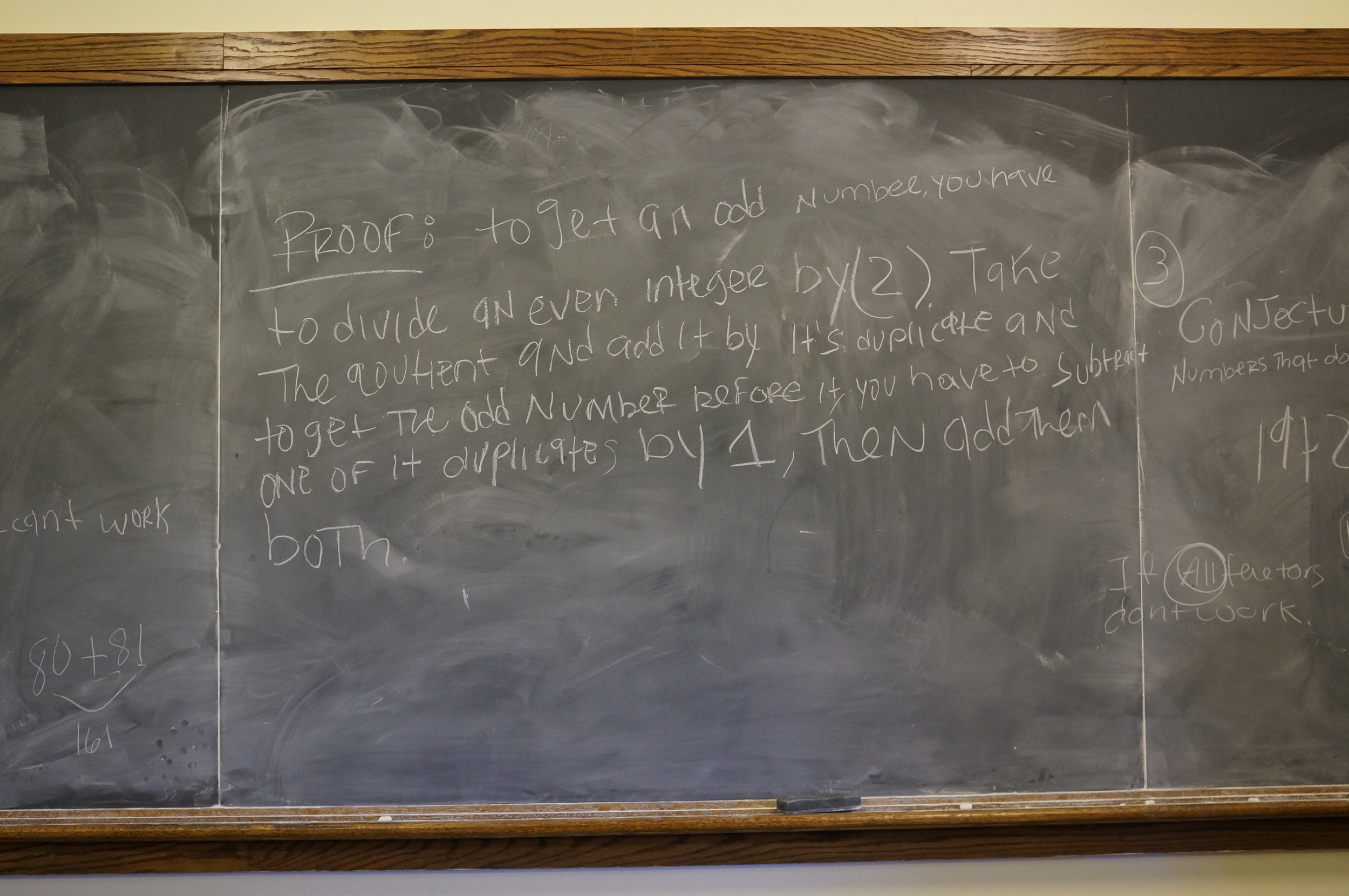Weeks 1/2: Solving Big Problems
As mentioned earlier, all BEAM students study problem solving throughout the program. Beyond Math Team Strategies, the other option is Solving Big Problems: working on the same problem for 2+ hours and really working to understand it.
In today's class, students investigated the following problem:
Which positive integers can be written as the sum of consecutive integers?
Students had a number of early conjectures, including:
- All odd integers have this property.
- If a given number is composed only of factors without this property, then that number also won't be possible to write as the sum of consecutive integers (so, if 4 = 1 * 2 * 2 and 1 and 2 are impossible, 4 is also impossible).
The class was quickly able to prove the first conjecture, and then spent the next 2 hours working on the second. Can you figure it out?