BEAM DISCOVERY COURSE INFORMATION
About Logical Reasoning
Why Logical Reasoning?
How do we help students use deductive reasoning to understand mathematics? Answering this question is the goal of the Logical Reasoning classes.
Our logic classes help students develop skills in deductive reasoning, case analysis, working methodically, and proof by contradiction. Additionally, students learn to carefully read mathematical writing to understand new kinds of math problems, all key skills for their future success in mathematics.
Different Classes
Students will choose between three or four Logical Reasoning courses, each based on a different type of logic puzzle as a "hook" for the students. In each course, students begin by developing their skills on the chosen logic puzzle, and then they transition to doing math questions that use those same skills. By drawing explicit connections between the two types of work, we hope that students will develop new ways of thinking about the situations they encounter.
BEAM Discovery is a flexible program, so there is a great deal of room for improvisation and creativity in the logic classes. We hope that you will help us develop these courses and to grow them out over time.
Detailed Overview
The Logical Reasoning course begins by solving classic logic puzzles which provide the core skills of the class: deductive reasoning, case analysis, working methodically, and careful reading. We also want to lay the groundwork for proof by contradiction: the idea that you can try a case and go until you see a contradiction; then you can return and rule out that case.
As students gain these skills on logic puzzles, they will transition to solving math problems using those same skills. By explicitly drawing out the relationship between the puzzles and the problems, we hope that students will see how clear logical reasoning plays a deep role in mathematics.
Although we've developed a basic outline for sample classes, we don't have detailed lesson plans or handouts for students. You will have the flexibility (and responsibility) for developing your day-to-day lesson plans, selecting problems, and creating handouts. We just provide an outline, so that all students get the core skills. Indeed, if you have an idea for doing things differently, please suggest it!
Prepackaged classes
Although the courses all end up in a similar place, there will be several flavors of the course, each based around different puzzles.
We have prepackaged courses available on various different puzzle types, which have been taught at BEAM Discovery before successfully. These courses are:
Truth, Lies, and Logic (has a focus on truthtellers and liars aka knights and knaves puzzles)
Math for Pirates (has a focus on logic riddles, particularly those using induction)
Cryptarithms and other Arithmetic Puzzles (has a focus on arithmetic puzzles)
Elementary, My Dear! (has a focus on matching riddles aka Einstein puzzles aka griddlers)
You are also welcome to propose developing your own curriculum and teaching from that (for example, we’ve had folks successfully teach logical reasoning through KenKen puzzles before, as displayed below, and would love to have that again!).
If you’re INTERESTED IN creatING your own curriculum
If you’re applying to create your own curriculum rather than teach a pre-packaged course, the second step in the process will be to create a course description about how you would teach your course. For the Logical Reasoning course, we will ask you to include:
A short description of how you would teach a particular logic puzzle. Each of the links above contains a puzzle you should use in your proposal. If you are proposing something else, please include a specific puzzle and then discuss how you would go over it within the course.
A short description of how you would teach a particular math problem. You may use the math problem provided in the descriptions or choose your own. How would you draw connections between solving this problem and solving the logic puzzle you chose?
LOGIC COURSE #1: KenKen PUZZLES
KenKen are puzzles somewhat like Sudoku. In an n-by-n KenKen, you must place the numbers 1 through n into the grid so that each row and each column has exactly one of each number in it. Additionally, the grid is divided into "cages" that have a mathematical operation and the value of applying that operation to the numbers in the cage (but the numbers can be plugged into the operation in any order). The numbers 1 through n must be inserted so that each cage comes out correctly.
You can see lots of examples here. (Although they're called "Inkies", presumably in order to avoid trademark infringement!)
How Are KenKen Valuable Mathematically?
Solving a KenKen requires strong deductive reasoning. The whole experience is essentially a sequence of placing numbers whose location you can deduce. It also requires experimentation with cases. Hence, proof by contradiction is embedded in the puzzles, because you will often conclude that a particular solution path is impossible. ("If I put a 3 here, then does it work or do I reach a contradiction?)
For example, the KenKen class might transition to solving this problem (from MATHCOUNTS 2010, Chapter Target Round #8):
How many ordered pairs of positive integers satisfy the equation 1 x + 1 y = 1 6 where x < y?
The analysis in this problem is very similar to KenKen, by systematically examining which numbers can work (and quickly ruling out other numbers). By drawing this distinction explicitly, students can see how to solve difficult problems.
KenKen have an additional benefit, which is that they reinforce basic arithmetic, especially using the prime factorization of a number to find all other factorizations. Although we appreciate this feature, it is not why we are so interested in using KenKen. A class should emphasize the logical reasoning and not the arithmetic!
How Might This Class Run?
Ultimately, the class is yours to run in whatever way you feel will best serves the students. Here is one potential timeline.
3 days: Introduce basics of KenKen. Students solve and deduce strategies, sharing their ideas with the class. Tricky concepts (see below) are covered explicitly as a group. Build up to more difficult puzzles.
2-3 days: Provide students with another logic-based puzzle (perhaps Slitherlink) where they can deduce solving strategies and translate the ideas of KenKen into a new environment. Unlike KenKen, do not go over the rules. Instead, give the students instructions they must figure out themselves. (Other logic classes have puzzles that are more language-intensive, emphasizing close reading; this is intended to make up for that difference.)
4-5 days (or however much time is left): Solve math problems that use deductive reasoning, case work, working methodically, and the idea of finding a contradiction to disprove an idea. Draw explicit parallels between these math problems and the methods used to solve logic puzzles previously.
Problems To Use
You can find numerous KenKen at this link. If you are submitting an application to teach this course, please use the first Ken-Ken at this link for your sample.
LOGIC COURSE #2: Truth, Lies, and Logic
In liar and truthteller puzzles, you're presented with a situation where you are speaking with people who either always lie or always tell the truth. They're often presented as an example where you are on an "island of knights and knaves," where knights always tell the truth and knaves always lie (and normals could either tell the truth or lie). You must make some deduction based on statements that various people on the island have said. A classic puzzle might be this one:
Among the three people A, B, and C, one is a knight, one is a knave, and one is a normal.
A says "I am normal."
Then B says "That is true."
Then C says "I am not normal."
What are A, B, and C?
How Are Liar and Truthteller Puzzles Valuable Mathematically?
The puzzles teach deductive logic and reasoning by cases directly. For example, in the puzzle above, we immediately deduce that A is not a knight, for a knight would never say "I am normal." If A were normal, then B can't be a knave, since they are confirming that A is telling the truth. This would make B a knight and C a knave. It is impossible for C to be a knave because C would be telling the truth when saying "I am not normal." Hence, A cannot be normal either, and we know that A is a knave. Already, we have seen case analysis, logical deduction, and an embedded proof by contradiction.
Additionally, liar and truthteller puzzles benefit close mathematical reading. They require strong attention to detail; one cannot simply read them looking for key phrases, and there is no "one way" to solve them. Students internalize the idea that statements can be given a truth value. Finally, they learn the mathematical meaning of "if" and how it differs from normal English usage.
For example, the Liar and Truthteller puzzle might transition to solving this problem (from the Math Kangaroo contest):
There are 50 bricks colored red, white, and blue in a box. The number of white bricks is eleven times the number of blue ones. There are fewer red ones than white ones, but more red ones than blue ones. How many of each color brick are there?
Reading each statement, understanding what makes it true, and then analyzing in a step-by-step fashion considering all cases is essential to this (and many other) math problems. By drawing this distinction explicitly, students can see how to solve difficult problems.
Liar and Truthteller puzzles can also be used to begin exploring the idea of mathematical proof (and false proofs) by analyzing an argument for the truth or falsehood of each statement.
How Might This Class Run?
Ultimately, the class is yours to run in whatever way you feel will best serves the students. Here is one potential timeline.
3 days: Solve several liar and truthteller puzzles, building up to more challenging variants. A good source is the book What is the Name of This Book? by Raymond Smullyan.
2 days: Depending on student progress, continue with the liar and truthteller puzzles or introduce another type of puzzle.
4-5 days (or however much time is left): Solve math problems that use deductive reasoning, case work, working methodically, and the idea of finding a contradiction to disprove an idea. Draw explicit parallels between these math problems and the methods used to solve logic puzzles previously.
Problems To Use
There are numerous examples of such puzzles online, but you can use the above puzzle for your application. We can provide copies of What is the Name of This Book? for the class.
logic course #3: MATCHING RIDDLES
What Are Matching Riddles?
Matching riddles are another classic logic puzzle. They generally present information about some situation and ask you (typically through deduction and a process of elimination) to figure out what objects belong to whom, or something along those lines. A classic example is Einstein's Riddle.
How Are Matching Riddles Valuable Mathematically?
While it is possible to solve a matching riddle through brute force by constructing a giant grid, it is much more instructive (and efficient) to make deductions about the puzzle through careful study. Making these deductions teaches students to find a point of attack on a complicated question, looking for the entry that allows the rest of the question to be understood and solved.
Additionally, students learn to methodically track their progress; to apply deductive logic; and to try multiple cases. By trying a case that fails, students get an introduction to proof by contradiction.
For example, you could follow up matching puzzles by doing problems like the one below that require students to work on steps carefully and keep track of them to find the answer.
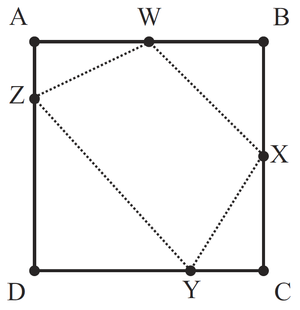
Square ABCD has sides of length 12 units each. Points W, X, Y, and Z lie on sides AB, BC, CD, and DA, respectively, so that AW = 1 2 AB, BX = 1 2 BC, CY = 1 3 CD, and AZ = 1 4 DA. What is the area of quadrilateral WXYZ? (See image below. From MATHCOUNTS 2010, Chapter Target Round #2.)
How Might This Class Run?
Ultimately, the class is yours to run in whatever way you feel will best serves the students. Here is one potential timeline.
3 days: Introduce basics of the riddles, and solve progressively more difficult riddles.
2-3 days: Move on to more challenging riddles, and introduce twists to them. For example, you might discuss the mathematical meaning of "if" and introduce riddles that use it, of the form, "If Mayra plays soccer, then Jossiel will not play soccer."
4-5 days: Solve math problems that use deductive reasoning, case work, working methodically, and the idea of finding a contradiction to disprove an idea. Draw explicit parallels between these math problems and the methods used to solve logic puzzles previously.
Problems To Use
In addition to Einstein's Riddle, many of these puzzles can be found by Googling terms like "Einstein riddles" or "grid puzzles". (For example, here are several more.)
About Creative Problem Solving
Why Creative Problem Solving?
The Creative Problem Solving courses are designed to introduce students to contest problem solving. There are two reasons we believe this can be so important for students.
First, contest-style problems challenge students to apply their mathematical knowledge in new ways. They cannot be solved using procedures alone, and so students must genuinely think about their mathematics knowledge to correctly solve them. It is our hope that students will make this transition in their mathematical thinking.
Second, math contests are a way for students to stay involved with mathematics beyond BEAM. After the summer, we can help students' schools register for math competitions for them. Moreover, there are numerous online tools that students can continue to use after the summer, and by starting them off on those tools now, they will be able to further their educations on their own.
Different Classes
Each Creative Problem Solving course is designed to equip students to do well in the MATHCOUNTS contest. The courses take shape by identifying common problem types and learning the mathematics to do well on those problems.
We believe that interesting content makes learning problem solving strategies more exciting. We furthermore believe that depth is more valuable than breadth to learn mathematics and how to do mathematics. Hence, Creative Problem Solving courses teach problem solving through the lens of a particular content area.
We have prepackaged courses available on several content areas, which have been taught at BEAM Discovery before successfully. These courses are:
Counting Without Counting (with a focus on combinatorics and the multiplication principle)
Primes, Powers and Solving Problems (with a focus on divisibility and prime factorization)
Unruly Patterns, Sequences, and The Rules That Govern Them (with a focus on sequences)
Words Meet Numbers: An Algebra Story (with a focus on algebraic work problems)
Of course, if you’d like to design your own curriculum, feel free to propose another area! For example, we’ve thought that geometry (with a focus on deriving angles and side lengths) might make a good course.
If you’re developing your own course, we do have many years of archived math contest problems and copies of Art of Problem Solving textbooks that you can use to plan your course. You will have the flexibility (and responsibility) for developing your day-to-day lesson plans, selecting problems, and creating handouts.
Other Important Notes
Remember that the goal of this course is to give students a start that they can build off of. Sometimes class will move slowly and might not cover as much as you hoped, especially because students might be missing important basic skills. If they feel empowered to continue learning on their own, then the class has been a huge success.
While we believe that competition can be healthy, it is not for everyone, and competitions often turn young people off from mathematics. To prevent this, it is important to emphasize how interesting the problems are and the learning that students are doing independent of winning or losing. The class should always maintain a positive atmosphere for all students and should not spotlight students who are particularly quick or solve more problems; everyone's progress should be celebrated.
Additionally, contests often emphasize speed to a much greater extent than speed is valuable when doing mathematics. While preparing students for the speed required on contests, your course should also emphasize that this is an artificial element of most math contests and that they should strive to do and enjoy the problems rather than to rush through. Please don't let students walk out thinking that speed is a measure of their mathematical skill!
IF YOU’RE INTERESTED IN CREATING YOUR OWN CURRICULUM
If you’re applying to create your own curriculum rather than teach a pre-packaged course, the second step in the process will be to create a course description about how you would teach your course.
For the Creative Problem Solving course, please include a specific problem, the context for teaching that problem (for example, what you might cover in before doing it), and how students would tackle that problem in class.
About Math Fundamentals
Why Math Fundamentals?
While our students are selected for the potential they show in abstract thinking and problem solving, we've found that certain basic skills are consistently missing from even the strongest students at many of our partner schools, to the point of preventing some students from pursuing more advanced work. Math Fundamentals is designed to fill in key gaps in skills, while building their conceptual understanding and broadening their perspective beyond algorithms.
In particular, students' backgrounds are often centered around procedural fluency, and as a result students can do only the specific types of problems they are used to. Math Fundamentals is a chance to break free of that, by exploring topics in mathematics and doing novel problems that require students to reflect on their knowledge.
DETAILed Overview
There are two key aspects to the Math Fundamentals course: the skills students get in interpreting mathematics, understanding definitions, and processing how subjects should connect to one-another, and the knowledge they gain in whatever topic they are studying. It is our hope that the course will help students in both ways. There is no way you can possibly cover all of the topics we want students to know, but you can model for them how they should be learning through a deep exploration of one topic.
We have both problems available that previously been used at BEAM, and copies of the Art of Problem Solving's Prealgebra book, which can provide additional problems. These problems are relatively sophisticated, and you may need some scaffolding to get to them, including more basic questions or some time to teach students directly. You may also want to include more motivation or applications for students. Ultimately, the course is yours to direct. You will have the flexibility (and responsibility) for developing your day-to-day lesson plans, selecting problems, and creating handouts.
Different Topics
Students will be placed into a Math Fundamentals course by considering both a pre-program assessment and their own preferences for what skills they want to strengthen.
Perhaps the biggest gap our students face is in their knowledge of fractions. Hence, any student whose fractions knowledge is weak will focus on that topic. At least one of the math fundamentals courses will definitely focus on fractions, for students who lack procedural fluency with fractions (for example, those who have not mastered adding fractions).
For students whose grasp of fractions is strong, there are several other possible Math Fundamentals courses for them to take. In addition to the main focus of the class, a Math Fundamentals course should cover other common difficulties that students face. Most notably, we want to give students a proper introduction to the meaning of the = sign.
We have a few prepackaged courses available, which have been taught at BEAM Discovery before successfully. These courses are:
Fractions, Puzzles, and Games (with a focus on building conceptual understanding of fractions)
Base Systems: Zeros, Ones, and Exploding Dots (with a focus on binary and place value systems)
Ratios and Rates (with a focus on ratios and rates)
You are also welcome to propose developing your own curriculum and teaching from that! For example, here are some potential courses with links to some example problems and material:
Fractions (but more advanced and conceptual) [sample problems 1, sample problems 2]
The Distributive Property and Mental Math Tricks [sample problems]
Exponents [sample problems]
Introductory Geometry.
An Important Note
Math Fundamentals is, in some sense, the course that is most in danger of "feeling like school". Although it is the closest to covering school topics, it is very important that students treat this course as an exploration of interesting problems. They should be constantly challenged and enjoying the greater depth of knowledge they are gaining about math that they thought they knew.
IF YOU’RE INTERESTED IN CREATING YOUR OWN CURRICULUM
If you’re applying to create and teach your own curriculum rather than teach a pre-packaged course, the second step in the process will be to create a course description about how you would teach your course. For the Math Fundamentals course, please include:
Within whatever topic you have chosen (fractions, exponents, distributive property, geometry, etc.), what do you expect would give students trouble? How would you help students overcome that difficulty?
A short description of how your classroom would lead students through a particular math problem, for example in the example problems above.
About Applied Math
Why Applied Math?
There are two core principles behind BEAM Discovery. The first is that students should be challenged, and should be introduced to new topics and ideas that go deeper into mathematics. The second is that students should desire to continue their studies of mathematics beyond the summer, gaining the skills to pursue their interests.
At heart, we're pure mathematicians who love math for its own sake and who believe that mathematics is intrinsically beautiful. However, neither of our goals can truly be accomplished without applied math. For one thing, we will be missing key ideas in math if students do not explore how it can be used in the world. Moreover, while some students may fall in love with pure mathematics as we have, many of them will be motivated more by seeing it used in the world.
There is also one particular idea that is too important to ignore: programming. An education in programming is hugely empowering for students, and a key to their future. Moreover, a good introduction to programming can give students the tools to continue programming on their own after the summer. We want to make sure that programming is an option for all of our students.
Different Classes
A key principle of BEAM is one of choice: we believe that students are more invested in their educations when they have control over what they are learning. To that end, we would like the students to be able to choose between several different courses to find the one that excites them the most.
Teaching Applied Math is an opportunity to exercise your creativity. We don't have any set topics in mind. Instead, we encourage new ideas that will really excite the students and allow them to explore deep ideas.
We have prepackaged courses available on various topics, which have been taught at BEAM Discovery before successfully. These courses are:
Voting Theory (on choice, fairness, and voting theory)
Big Questions and Big Answers (on statistics and data with a focus on Fermi problems and estimations)
Game Theory (on game theory covering a little of both combinatorial games and rational decision making, including prisoner's dilemma)
Primes and Programming (on programming in Python and number theory)
You are also welcome to propose developing your own curriculum and teaching from that. For example, some other topics:
Programming with a different focus. We might offer multiple options within programming. The prepackaged course is a bit more series and uses Python, but other students might choose a more mellow introduction in a block-based environment such as Scratch or code.org, where they can build functional, graphical applications quickly. (The challenge with block-based programming is to make sure students are still challenged and really learning the logical flow rather than trying a bunch of things until something stick.)
Astrophysics. An astronomy or astrophysics course could talk about the positions of stars and planets and celestial navigation; it could talk about how similar triangles are used to measure the distances to stars through parallax; it could present various formulas, show some evidence for their validity, and then use them to derive more about the stars. Mathematical content would include both scientific notation, units of distance, and how to plug numerical values into formulas, all of which would be very valuable to students.
Mathematical Biology. A biology course could introduce students to genetics and do various mathematical analyses of how traits are passed down and how likely various conditions are depending on the genetic makeup of the parents. It could discuss the differences between asexual reproduction and sexual reproduction, demonstrating how genetic diversity can be increased. (Yes, there will be jokes.) It could discuss DNA, how data is encoded into DNA, and how many possibilities can exist from a single DNA strand.
Circuit Design. A circuit design course could introduce logical circuits, AND, OR, and NOT gates, and equivalences between different combinations of gates. Students could construct different gates and, after an introduction to binary, perhaps get to the point of building an adder. Actual opportunities to construct real circuits could give let them bring their ideas into the world.
Cryptography. A cryptography course could discuss modular arithmetic as well as probability when looking at the likelihood of different codes being broken. (Although, it is unlikely you'd have time to get to RSA encryption.)
In short, there are a wealth of interesting applied courses that cover deep material and are accessible to rising 7th graders.
Unlike most of the other courses, there is no specific roadmap to Applied Math. We want to see students getting excited about a topic, ideally so that they will want to pursue continued study of it in the future. Moreover, seeing how math is used directly can give them a much stronger sense for mathematics as a subject, and how it must fit together.
IF YOU’RE INTERESTED IN CREATING YOUR OWN CURRICULUM
If you’re applying to create your own curriculum rather than teach a pre-packaged course, the second step in the process will be to create a course description about how you would teach your course. For the Applied Math course, please include:
Briefly describe the course and what you would cover.
Tell us about something exciting that might happen in the classroom.
What is a problem that the students might solve? What is a project they might do?