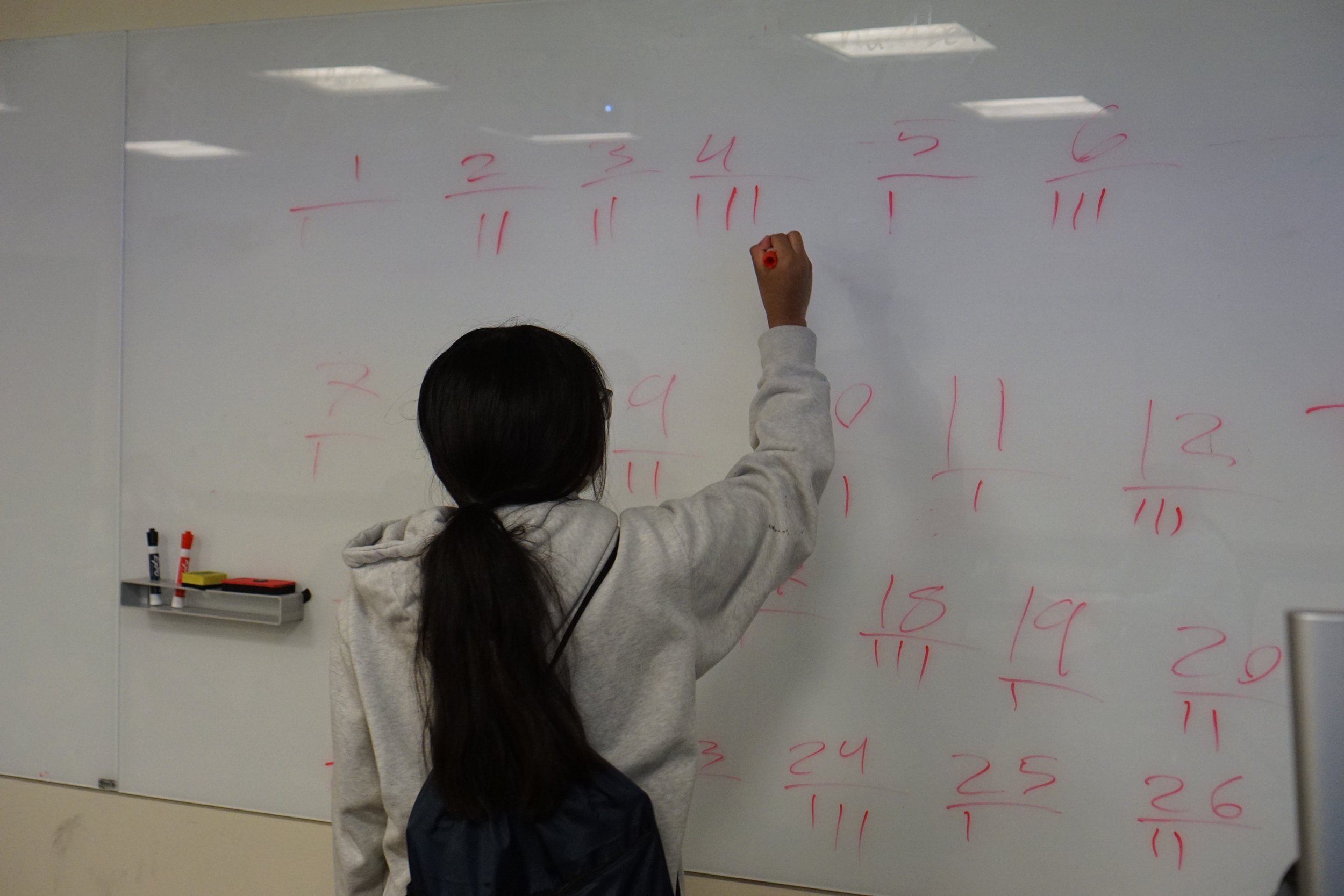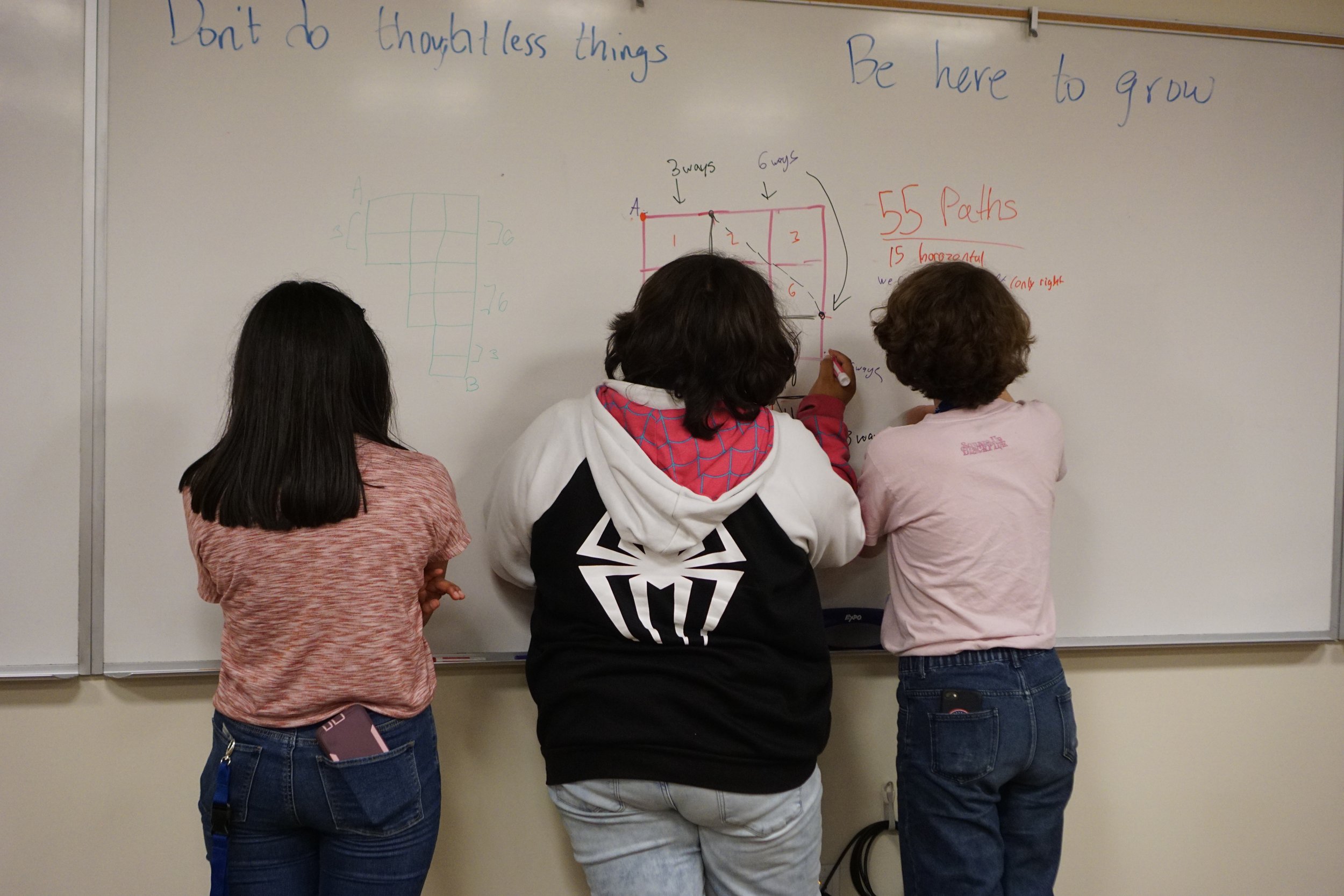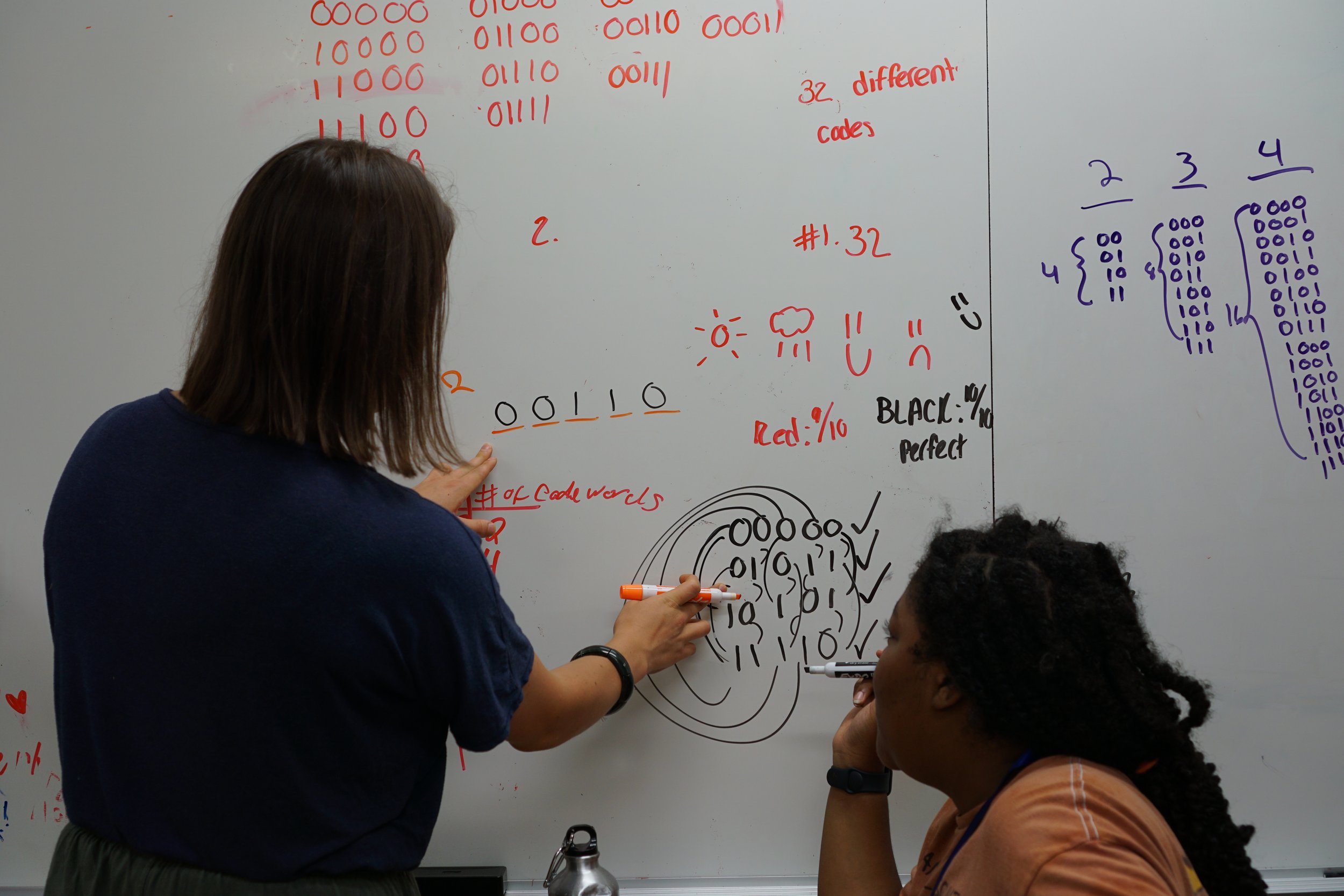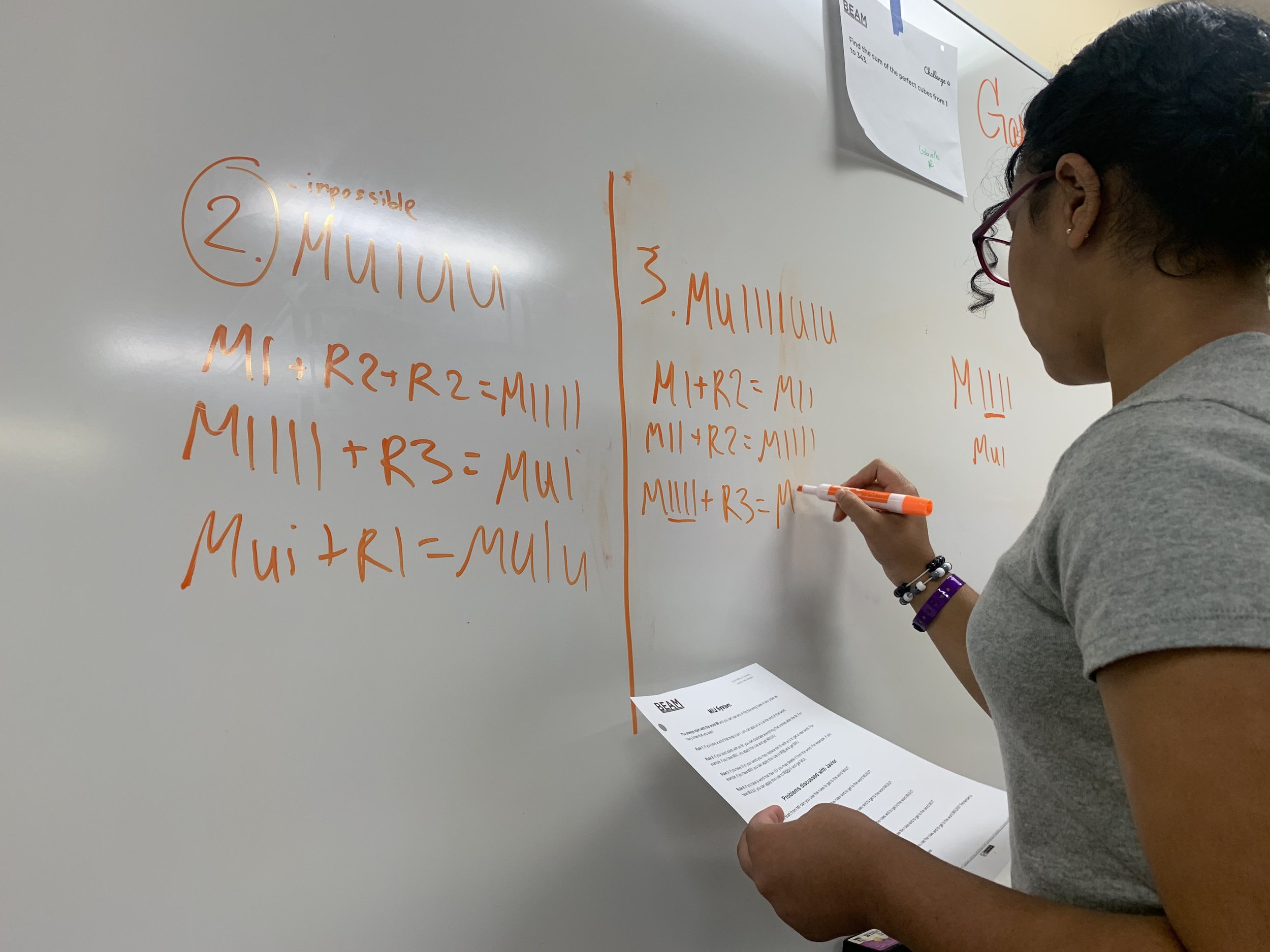How do mathematicians know that a particular fact is true? For example, how do we know for certain that there are infinitely many prime numbers? It's because we found a proof of that fact: starting from the basics of math, we built out logical reasons for why there must be infinitely many primes. Proofs can be beautiful and elegant, but they also form the underpinning of math, and for students they're a great step to develop rigorous thinking and to work more like a mathematician.
How, then, can we ensure that students develop the skills to create their own proofs? This past summer, at our Summer Away site at Union College, BEAM piloted a new Introduction to Proofs course developed and taught by BEAM’s Learning and Pedagogy Manager, Javier Ronquillo Rivera.
“One of the main goals of the courses at BEAM Summer Away is getting students to start owning the process of proving things mathematically. This involves not only understanding the content that the class is covering, but also developing some habits of mind (and naming them) that mathematicians use every day. For example, looking at patterns, making conjectures from those patterns, trying to find counterexamples, or trying to find ways of being certain that the pattern always holds,” said Javier. “We decided to run this pilot to ensure that every student has the opportunity to develop the habits of mind and to have a common language around them.”
In the second half of the week-long class, Javier introduced the class to the MU puzzle, created by Douglas Hofstadter (and presented in Godel, Escher, Bach). The puzzle contains the letters M, I, and U, which can be combined to produce strings of letters. The solver is asked to start with the string MI and transform it into the string MU using one of four rules in each step. (Spoiler alert: the puzzle can’t be solved. The rules and more here.)
Javier explained, “By introducing this puzzle before developing the tools to prove its impossibility, there were two things I hoped the students would understand and feel: The first one is understanding the subtle difference between knowing that a result is impossible versus having tried many ways of getting to that result and not being able to. In the MU puzzle — without having completely developed the tools needed to prove the impossibility — we fall in the space of saying: ‘Is it really impossible to get the MU word, or have we just not found a way to get there by using the rules we have?’ I call the students’ attention to that uncertainty to show that in order to avoid that feeling, we need proof. The second thing I hoped students would feel, while using the tools we had at that time, is the need for mathematical proof.”
The puzzle stuck with Zayden, who wrote, “Although ‘MU’ is impossible, I built a connection that taught me to see patterns in these problems that I never saw before.” Andrew also reflected, “[I] worked on this for a while…it was very interesting because there are so many ways to try to come up with a solution.”
Led by Javier, students discussed their own definitions of arithmetic properties like even, odd, and divisible. Students explored how utilizing slightly different definitions led to different results, and collaborated to create strong definitions that required abstraction. For example, taking the definition “An even number is divisible by 2” and strengthening it to “An integer n is even if and only if n is twice some integer.” With these strong definitions, they were able to answer a variety of questions about different integers, included in the video below!
Visit Javier’s class [10 minutes].
BEAM Pathway students mentor a new cohort of mathematicians