Happy Pi Day!
Happy 𝝅 Day! We’re celebrating with Reuleaux polygons and the remarkable property that ties them to 𝝅. We’ll also take a look at some of the many applications of these interesting shapes, touch on some big mathematical results, and even share a few open questions in the world of Reuleaux polygons!
Reuleaux Polygons and 𝝅
A Reuleaux triangle is a "curve of constant width." That just means that whenever you hug them with two parallel lines, they're always the same width apart:
Because of that, you could use them as wheels or in a whole bunch of other places where you might "normally" use a circle (or where circles won't do, like a drill that makes square holes). More on that below!
You can build a Reuleaux triangle by taking three intersecting circular discs, each with its center on the boundary of the other two, like this:
Alternatively, you can think of it as an equilateral triangle where each side of the triangle has been replaced with a circular arc whose center is on the opposite vertex.
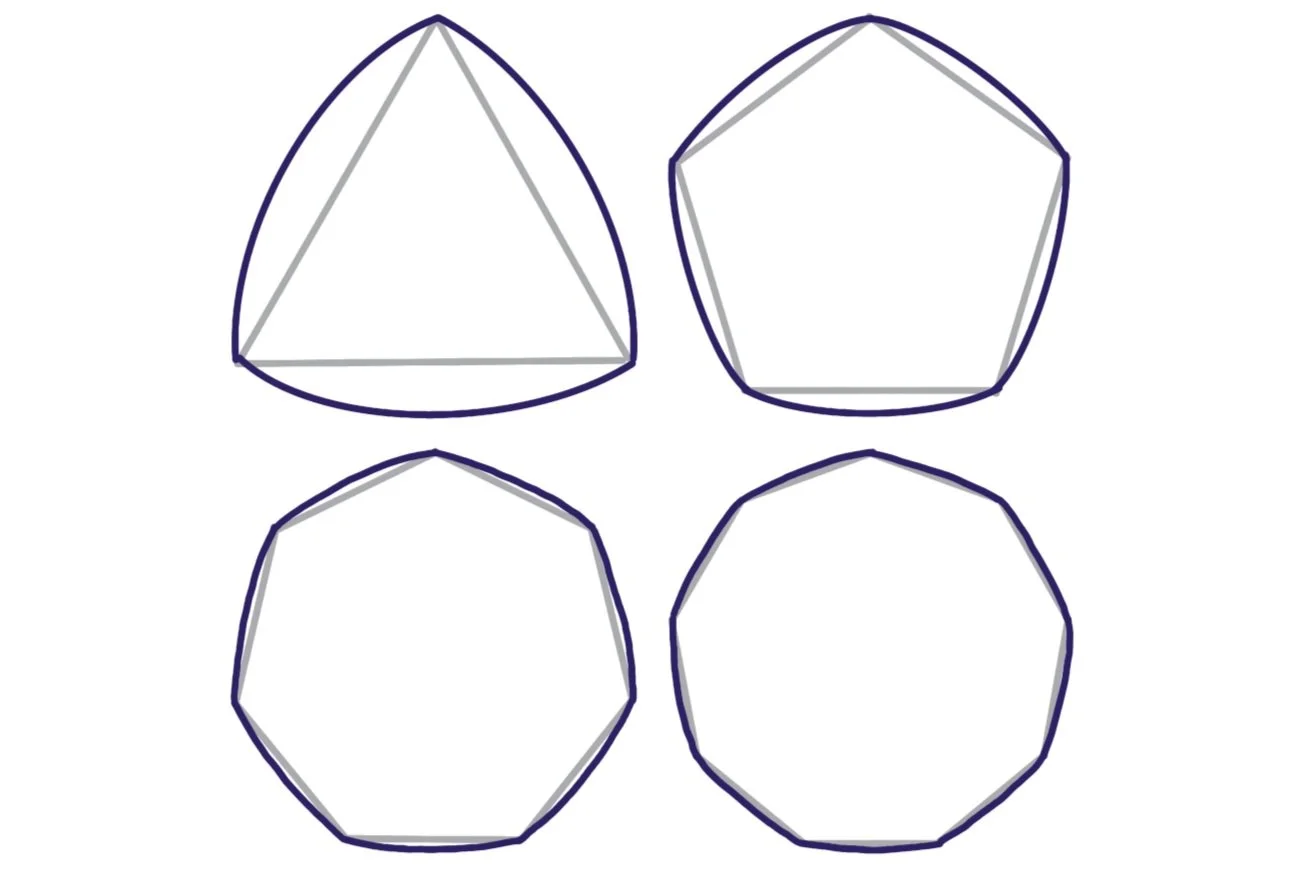
But, it’s not only triangles! There are infinitely many Reuleaux polygons which we can build in a similar way. Start with any regular polygon with an odd number of sides, replace each edge with a circular arc whose center is on the opposite vertex, and voila — you have yourself another Reuleaux polygon!
So what about this connection to 𝝅? Well, it’s not too different from a circle’s. You probably know the formula for finding the circumference of a circle:
c = πd
Divide by d to get c/d= π. This gives us a fundamental property of circles: when you divide the length around by the diameter, you always get π no matter the size of the circle.
For a Reuleaux triangle, we refer to the perimeter p instead of the circumference, and we talk about the width w instead of the diameter. (These are just different names for the same concepts.) To find the perimeter, notice that the angle at the vertex of an equilateral triangle is 60 degrees. Then the arc on the opposite side of the triangle is 1/6 of the way around a circle with a radius of w. Because the whole circumference would be 2wπ, that means that the length of that arc is:
2wπ/6 = (π/3)w
Add up all three arcs that make the Reuleax triangle, and you get πw for its perimeter.
Divide that by the width, and we find that:
p/w = πw/w = π
This means that, amazingly, Reuleaux triangles have the same relationship with π that a circle has! In fact, the same calculation works if we start with ANY regular n-gon where n is odd, so really this relationship holds for ALL Reuleaux polygons. (Read on to discover an even bigger generalization of this result.)
Applications
The fact that Reuleaux polygons are curves of constant width makes them popular for use in various settings. Since they roll nicely, coins that are the shape of a Reuleaux polygon can still be used in vending machines! Some examples include the Canadian Loonie (a Reuleaux 11-gon) and the 2 pula coin from Botswana (a Reuleaux 7-gon).
Like with the commonly used circular manhole covers, the constant width of Reuleaux polygons means that with just a small lip underneath, they can’t fall into the holes that they are made to cover.
Photo by Owen Byrne
So why aren’t they commonly used as manhole covers? Well, if you need to roll them on their side, the center of gravity makes them harder to roll… But that’s exactly the property that makes them desirable for making pencils with a Reuleaux cross-section. These ones will be less likely to roll off your desk.
Similarly, a fire hydrant valve in the shape of a Reuleaux triangle can be helpful in preventing mischief, since you’ll need a special tool to get it open.
Spot the Reuleaux triangle bolt head?
Reuleaux triangles also have a really cool relationship to squares! They can form a rotor within a square, that is, they do a full rotation inside the square while maintaining contact with all four sides.
In the early 1900’s, the Watt’s Brothers Tool Works used this relationship to patent a drill bit that can drill square holes! You can view the original patent!
And if you’re wondering where these shapes get their name, it comes from Franz Reuleaux (1829-1905), the German mechanical engineer who studied and designed mechanisms that convert rotation around a fixed axis into a back-and-forth or up-and-down motion. One of the possible applications is a film advance mechanism, like the one seen here:
Bigger Math Results and Open Questions
Barbier’s Theorem, first published in 1860, showed that every curve of constant width has the same relationship to what we’re celebrating today, namely, p/w= π.
Wondering about the area of a Reuleaux triangle? It’s known to be 1/2(π-√3)w2. If you’d like to try deriving it yourself, you might consider breaking it into an inner equilateral triangle and the three curvilinear regions formed between this triangle and the circular arcs.
The Blaschke–Lebesgue Theorem proves that the Reuleaux triangle has the smallest area of all curves of a fixed constant width.
And if you’re looking for open questions…
The optimal packing density of Reuleaux triangles in the plane is conjectured but unproven!
In 3-dimensions, it’s unknown which surfaces of constant width have the smallest volume!
Or maybe you’d just like to see some surfaces of constant width in action — check out this cool video from Numberphile!