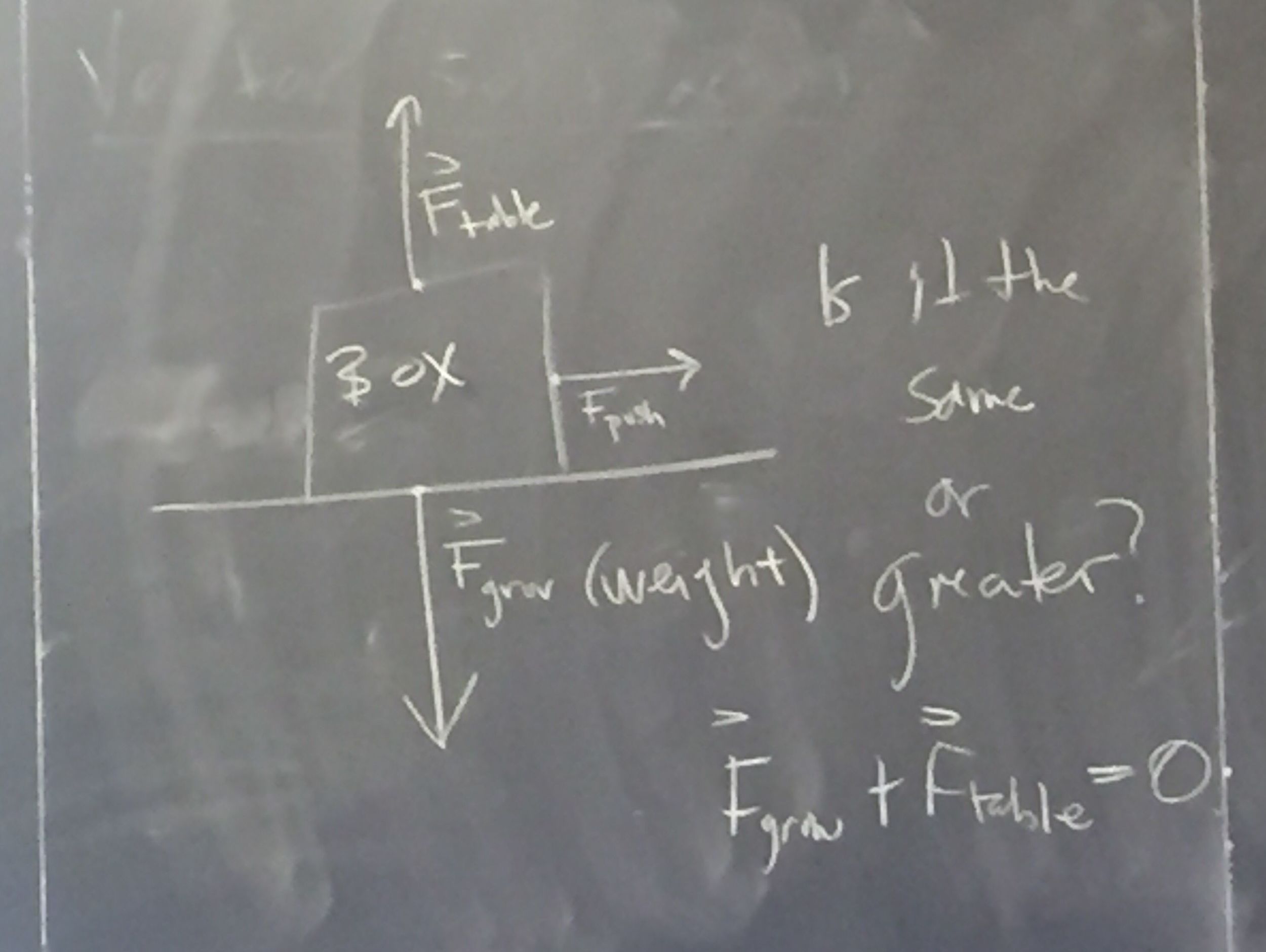Week 3 Class: Aerodynamics
This is a guest post by Matt Weber, our Math Team Strategies instructor.
I walk into Cory Colbert’s Aerodynamics class and find the students working on vector addition and subtraction, a topic not normally taught till 11th grade Pre-Calculus. A discussion among one group of three strikes me as highly representative of the BEAM attitude: a problem has asked them to “verify” a particular property of vectors, but one student, a veteran of the Proofs class from the first week, is not satisfied with the single numerical example they have used. We get into a discussion of the difference between verifying with a numerical example and truly proving something: since this class is geared more towards pragmatic applications, verification is enough—for now, anyway.
Cory is having the students work through several examples using both a geometric representation of the vector combinations on a graph, and a purely numerical approach. The point is to show that they have the same result, so that the students can feel comfortable using the “shortcut” of just adding or subtracting the vector components—even without a formal proof, it’s a robust way of making sure that at BEAM, no one is ever asked to accept something solely on the teacher’s say-so. This program gives teachers and students alike enough space and time not to rush, to become comfortable enough with one set of tools to be able to use them fluently in new situations.
Speaking of which: why is Cory teaching this particular topic? After the students reassemble from a short break, he reveals the reason, with a presentation on the relationship between vectors and forces. (“What’s a force?” Cory asks. “...I will accept at most one Star Wars reference.” A student quickly obliges by quipping that the answer is “Yoda.”) The class settles on the idea that forces cause objects to move.
There are two pairs of opposing forces acting on a plane in flight: lift versus gravity, thrust versus drag. He starts with a discussion of gravity, neatly dodging a potential derailment about whether or not the “theory of gravity” has actually been “proven.” And this is why they need to understand vectors, to represent these four forces. A student question gets at the heart of the matter: “How does it generate lift if the propellers are on the side?”
A brief discussion ensues, covering space travel, escape velocity, aerodynamics, and related matters. One student mentions that it takes much less fuel to get from orbit around the Earth to the Moon, than it did simply to leave Earth and get into orbit around it. Cory says that by the end of the class, they will be able to explain why. But the immediate next topic is to understand why a box resting on a table doesn’t move, if the force of gravity is the only force acting on it. This is a surprisingly subtle question, since we don’t normally think of tables as exerting an upward force—but they do! Meanwhile, Cory’s provocative questions lead the students to, in essence, figure out Newton’s Laws of Motion for themselves, at least in a qualitative sense. After vectors, these Laws are the crucial next waypoint in their flight of discovery.